Open vragen hoofdstuk 1 |
| 1 |
Combinaties van bits
|
| a. |
Met 8 bits kun je 256 verschillende waarden maken.
Hoeveel verschillende waarden kun je met 4 bits maken.
Met 4 bits kun je 24=16 waarden maken
|
| b. |
Hoeveel verschillende waarden kun je met 10 bits maken.
Met 10 bits kun je 210=1024 waarden maken
|
| c. |
Hoeveel verschillende waarden kun je met 16 bits, dus met twee bytes, maken.
Met 16 bits kun je 216=65536 waarden maken
|
| d. |
Welke machten van twee komen er vaak in advertenties van computers voor, bij welke onderdelen?
De hoeveelheid intern (en extern) geheugen zijn bijna altijd machten van twee. Bijv. 256 MB of 512 MB RAM (256 = 28 en 512 = 29)
|
| 2 |
Van binair naar decimaal
|
| a. |
Schrijf de decimale notatie van het binaire getal 00100101
1 + 4 + 32 = 37
|
| b. |
Doe hetzelfde voor het binaire getal 10011110
2 + 4 + 8 + 16 + 128 = 158
|
| c. |
Doe hetzelfde voor het binaire getal 11111010011
1 + 2 + 16 + 64 + 128 + 256 + 512 + 1024 = 2003
|
| 3 |
Van decimaal naar binair
|
| a. |
Schrijf het decimale getal 63 als binair getal
00111111
|
| b. |
Schrijf het decimale getal 185 als binair getal
10111001
|
| c. |
Schrijf het decimale getal 1000 als binair getal (je hebt dan meer dan 8 bits nodig)
1111101000
|
| 4 |
Vermenigvuldigen met 2 en delen door 2
|
| a. |
Vermenigvuldig het binaire getal 01101111 met 2. Wat is de uitkomst (binair)?
01101111 × 2 = 11011110
|
| b. |
Hoe kun je dat (zonder te rekenen) zo opschrijven?
Aanwijzing: Als je een decimaal getal met 10 vermenigvuldigt schrijf je dat zo op, hoe doe je dat ?
Gewoon een 0 achter het getal schrijven (net zo als je een decimaal getal vermenigvuldigt met 10)
|
| c. |
Is het binaire getal 100110010101 een even of een oneven getal. Waaraan kun je dat snel zien?
Het binaire getal eindigt op een 1, dus dan is het oneven.
|
| 5 |
Van hexadecimaal naar decimaal en omgekeerd
|
| a. |
Schrijf het hexadecimale getal 63 als decimaal getal
16 × 6 + 3 = 99
|
| b. |
Schrijf het hexadecimale getal A2 als decimaal getal
10 × 16 + 2 = 162
|
| c. |
Schrijf het hexadecimale getal FF als decimaal getal
255
|
| d. |
Schrijf het decimale getal 87 als hexadecimaal getal
57
|
| e. |
Schrijf het decimale getal 108 als hexadecimaal getal
6C
|
| f. |
Schrijf het decimale getal 206 als hexadecimaal getal
CE
|
| 6 |
Van hexadecimaal naar binair en omgekeerd
|
| a. |
Schrijf het binaire getal 10101010 als hexadecimaal getal
AA
|
| b. |
Schrijf het hexadecimale getal BB als binair getal
10111011
|
| c. |
Schrijf het binaire getal 11111111 als hexadecimaal getal
FF
|
| d. |
Schrijf het hexadecimale getal 11 als binair getal
10001 (of 00010001)
|
| 7 |
Moeilijker gevallen
|
| a. |
Schrijf het binaire getal 1100110011 als decimaal getal
1 + 2 + 16 + 32 + 256 + 512 = 819
|
| b. |
Schrijf het decimale getal 999 als binair getal
999/2=499 rest 1, 499/2=249 rest 1, 249/2=124 rest 1, 124/2=62 rest 0, 62/2=31 rest 0, 31/2=15 rest 1, 15/2=7 rest 1, 7/2=3 rest 1, 3/2=1 rest 1, 1/2=0 rest 1, schrijf nu de resten achter elkaar in omgekeerde volgorde: 1111100111
|
| c. |
Schrijf het decimale getal 999 als hexadecimaal getal
999/256=3 rest 231, 231/16=14 rest 7, antwoord: 3E7 (256 = 162 en 14 wordt E)
|
| d. |
Schrijf het hexadecimale getal 2AE als decimaal getal
2 × 162 + 10 × 16 + 14 = 686
|
| e. |
Schrijf het binaire getal 0101111100111011 als hexadecimaal getal
5F3B (zie vraag 7f)
|
| f. |
Schrijf het binaire getal 01011111 als hexadecimaal getal, schrijf ook binaire getal 00111011 als hexadecimaal getal.
Schrijf daarna die twee hexadecimale getallen achterelkaar. Als het goed is krijg je hetzelfde getal als bij 7e
Verdeel het in twee groepjes van 8
01011111=5F (hex) en 00111011=3B (hex), dan wordt het 5F3B (zet de twee hexadecimale getallen gewoon achter elkaar)
|
| g. |
Schrijf het hexadecimale getal 81A3 als decimaal getal
8 × 163 + 1 × 162 + 10 × 16 + 3 = 36387
|
| 8 |
Binair optellen
|
| a. |
Bereken 00100101 + 10011110 (het zijn binaire getallen) zonder er eerst decimale getallen van te maken
00100101 + 10011110 = 11000011
|
| b. |
Bereken 11101 + 1011 (het zijn binaire getallen) zonder er eerst decimale getallen van te maken
11101 + 1011 = 101000
|
| c. |
Bereken 01110011 + 11000111 (het zijn binaire getallen) zonder er eerst decimale getallen van te maken
110110 + 01111111 = 11110101
|
| d. |
Bereken ................................
100111010
|
| e. |
Het resultaat van 8d past niet in één byte. Hoe wordt dat genoemd?
De uitkomst bestaat uit 9 bits: 100111010
Het past dus niet in een byte. Wanneer je het antwoord in een enkele byte zet dan valt het voorste bit weg en wordt de uitkomst 00111010. Er is dan overflow opgetreden, vergelijkbaar met het over de kop gaan van een kilometerteller.
|
| f. |
Welke uitkomsten uit 8a, 8b en 8c zijn even?
8b: 101000 is een even getal (want het is 40 dec), dat kun je zien aan de laatste 0
|
| 9 |
De two's complement methode voor negatieve getallen
|
| a. |
Tel de binaire getallen 00001001 en 11110111 op (Je krijgt overflow, schrijf alleen de laatste 8 bits op, gooi het voorste bit weg)
Optellen levert acht nullen, met een 1 ervoor (dat is een overflow bit). Als we dit gewoon weggooien komt er dus 0 uit.
|
| b. |
Tel op dezelfde manier de binaire getallen 01010101 en 10101011 op
Hetzelfde als bij 9a
|
| c. |
Het decimale getal 144 is binair 10010000. Draai alle bits om (verander de 1 in 0, en de 0 in 1), dan krijg je 01101111. Tel daar 1 bij op. Welk binair getal krijg je dan? En wat komt er uit als je dat bij het eerste getal, dus 10010000, optelt? Dat nieuwe getal is de binaire presentatie van -144!
01110000 10010000 + 01110000 = (1)00000000
|
| d. |
Welk binair getal moet je bij 10110011 optellen om er 0 (dus 00000000) uit te krijgen?
Alle nullen en enen omdraaien, dan krijg je: 01001100 en bij dat getal 1 optellen: 01001101
|
| e. |
Schrijf het decimale getal -84 als binair getal (met de twee-complement methode)
84 = 1010100, alle bits omdraaien, dan krijg je: 0101011
Bij dat getal 1 optellen, dan heb je het antwoord. Dus -84 = 0101100
|
| 10 |
Negatieve binaire getallen
|
| a. |
Schrijf -75 als binair getal (zie opg. 9)
Eerst 75 = 01001011, dan alle bits omdraaien, dan krijg je 10110100
Daar 1 bij optellen, dan krijg je 10110101, dus -75 = 10110101
|
| b. |
Schrijf 120 als binair getal
120 = 01111000
|
| c. |
Bereken binair -75 + 120.
Welk binair getal komt er uit. En klopt het met de decimale getallen?
10110101 (= -75)
01111000 (= 120)
----------- +
00101101 (= 45 klopt !)
|
| 11 |
Schakelingen
|
| a. |
Teken de schakeling voor een en-poort
en-poort 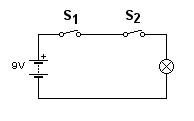
|
| b. |
Teken de schakeling voor een xof-poort
xof-poort (ook wel hotelschakeling genoemd) 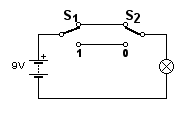
|
| c. |
Maak een tekening van de schakeling met één en-poort en één xor-poort voor de optelling van twee 1-bits getallen
schakeling voor de optelling van twee bits 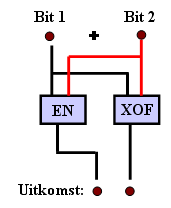
|
| 12 |
Schakelingen maken met LogicalSim (Alleen als je je verveelt)
|
| a. |
Start LogicalSim, klik op tabblad EN, en ontwerp de schakeling met een en-poort en een lamp.
Dat doe je als volgt:
LogicalSim: hier downloaden
- Klik op het icoontje voor een schakeling:

Dan verschijnt er een en-schakeling op het tekenblad. Als je op die en-schakeling klikt verandert hij in een
andere schakeling, zo kun je alle schakelingen er mee krijgen. Klik net zo vaak tot het weer een
en-schakeling is, en versleep die schakeling een eindje naar rechts.
- Klik op het icoontje voor een bit:

Er verschijnt een bit op het tekenblad. En er verschijnt een venstertje, waarin om een titel gevraagd wordt. Vul daar bit 1 in, en klik op OK. Dan zie je bit 1 in de linker boverhoek en de waarde ervan is 0, want het rode lichtje is donker. Als je er op klikt wordt
de waarde 1, want dan gaat het rode lichtje branden. Als je er dan weer op klikt wordt de waarde weer 0.
- Klik nog eens op het icoontje voor een bit:

In het venstertje, waarin om een titel gevraagd wordt, vul je bit 2 in, en dan klik je op OK. Versleet bit 2 een eindje naar beneden, want anders staat hij boven op bit 1
- Klik op het icoontje voor een connector ( = verbindingsdraad) :
Er verschijnt een connector op het tekenblad. Versleep het rode uiteinde naar bit 1, en het groene uiteinde naar de linker kant van de en-schakeling.
- Klik nog eens op het icoontje voor een connector :

Er verschijnt een nieuwe connector op het tekenblad. Versleep het rode uiteinde naar bit 2, en het groene uiteinde naar de linker kant van de en-schakeling.
- Klik op het icoontje voor een lamp :

Er verschijnt een lampje op het tekenblad. En er verschijnt een venstertje, waarin om een titel gevraagd wordt. Vul daar uitkomst in, en klik op OK.
- Klik op het icoontje voor een connector ( = verbindingsdraad) :

Er verschijnt een connector op het tekenblad. Versleep het rode uiteinde naar naar de rechter kant van de en-schakeling, en het groene uiteinde naar de lamp.
- Dan is de schakeling klaar, en hij ziet er als volgt uit:
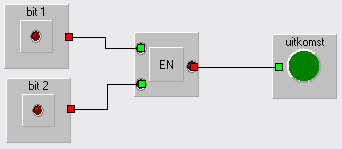
- Controleer of het goed werkt. Door op bit 1 en bit 2 te klikken kun je de waarde veranderen, en de uitkomst (de groene lamp) gaat soms branden.
In welk geval (bij welke waarden van bit 1 en bit 2 gaat hij branden?
|
| b. |
Start LogicalSim, klik op tabblad XOF, en ontwerp de schakeling met een XOF-poort en een lamp. En controleer of hij goed werkt aan de hand van de waarheidstabel.
De schakeling moet er als volgt uitzien: 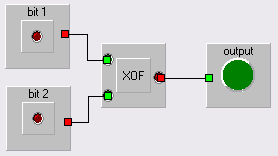
|
| c. |
Start LogicalSim, klik op tabblad EXTRA, en ontwerp de schakeling met een EN-poort en een XOF-poort en twee lampen en twee bits voor de optelling van twee 1-bits getallen. En controleer of het goed werkt.
De schakeling moet er als volgt uitzien: 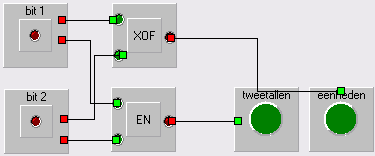
|
| d. |
Start LogicalSim, klik op tabblad EXTRA, en ontwerp de schakeling met EN-poorten en XOF-poorten en een OF-poort en twee lampen voor de optelling van drie 1-bits getallen. En controleer of het goed werkt.
De schakeling moet er als volgt uitzien: 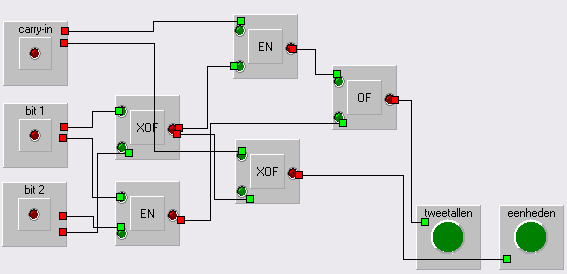
|
| 13 |
Binair vermenigvuldigen (Alleen doorlezen)
|
| a. |
Je kunt een binair getal vermenigvuldigen met 2 door een 0 achter het getal te zetten. Er is een schakeling die dat doet, en die wordt Arithmetic Shift Left genoemd (ASL) (deze schakeling schuift de bits een plek naar links, en zet een 0 in het laatste bit dat is vrijgekomen).
Hoe kun je de ASL-schakeling gebruiken om een binair getal met 4 te vermenigvuldigen?
De ASL-schakeling twee keer op het getal toepassen
|
| b. |
Beschrijf hoe je met optellen en Arithmetic Shift Left een vermenigvuldiging van binaire getallen kunt maken. Bekijk bijvoorbeeld de vermenigvuldiging 13 x 27, in binaire notatie 1101 × 11011.
Aanwijzing: 13 × 27 = (8+4+1) × 27
1101×11011 = 1000×11011 + 100×11011 + 1×11011 = 11011000 (3 nullen toevoegen, dus 3 keer ASL) + 1101100 (2 nullen toevoegen, dus 2 keer ASL) + 11011
|
| 14 |
Tabellen bij schakelingen met twee componenten
|
| a. |
Vul voor de schakeling hieronder de tabel in.
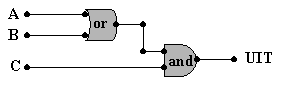
Als de lamp brandt geldt UIT = 1, en anders geldt UIT = 0
| A | B | C | UIT |
| 1 | 1 | 1 | |
| 1 | 1 | 0 | |
| 1 | 0 | 1 | |
| 1 | 0 | 0 | |
| 0 | 1 | 1 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 | |
| 0 | 0 | 0 | |
| A | B | C | UIT |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
|
| b. |
Beschrijf hoe je met optellen en Arithmetic Shift Left een vermenigvuldiging van binaire getallen kunt maken. Bekijk bijvoorbeeld de vermenigvuldiging 13 x 27, in binaire notatie 1101 × 11011.
Aanwijzing: 13 × 27 = (8+4+1) × 27
| A | B | C | UIT |
| 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
|
| c. |
Beschrijf hoe je met optellen en Arithmetic Shift Left een vermenigvuldiging van binaire getallen kunt maken. Bekijk bijvoorbeeld de vermenigvuldiging 13 x 27, in binaire notatie 1101 × 11011.
Aanwijzing: 13 × 27 = (8+4+1) × 27
| A | B | C | UIT |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
|
| 15 |
ASCII-codes m.b.v. tabel
|
| a. |
Wat is de ASC-code van het vraagteken?
Na opzoeken in tabel: 63 (dec) en 00111111 (binair)
|
| b. |
Welke delen van de ASC-tabel zijn gereserveerd voor de 26 letters van het alfabet?
A t/m Z: 65 t/m 90 en a t/m z: 97 t/m 122
|
| c. |
De ASC-codes van de tekens voor de cijfers 0 tot en met 9 verschillen van de getallen 0 tot en met 9. Wat is het verschil? Geef de binaire code voor het cijfer 9 en voor het getal 9
0 t/m 9 hebben de ASC-codes 48 t/m 57
Het cijfer 9 heeft ASC-code 57 (dec) en 00111001 (binair), het getal 9 is binair 00001001
|
| d. |
Wat is de ASC-code van het Tab-teken?
9
|
| e. |
Noem enkele veel voorkomende tekens die niet in de ASC-tabel voorkomen.
€ en © en ±
|
| 16 |
UNI-code en ASC-code
|
| a. |
Hoeveel tekens kun je met de ASC-code coderen? Hoe kun je dat aantal berekenen?
Met de asc-code: 256 tekens (28 = 256)
|
| b. |
Hoeveel tekens kun je met de UNI-code coderen? Hoe kun je dat aantal berekenen?
Met de uni-code: 65536 tekens (216 = 65536)
|
| c. |
In 1998 is het symbool van de euro toegevoegd. Wat is de UNI-code van het euro-symbool?
De unicode voor het euro-teken is 20AC (hex)
Je kunt het euroteken ook krijgen door op het numerieke toetsenbord 0128 in te tikken, terwijl je de Alt-toets ingedrukt houdt.
|
| 17 |
Digitaliseren van geluid
|
| a. |
Leg uit hoe geluid gedigitaliseerd wordt.
Geluid bestaat uit golven. Bij de geluidsgolven wordt met regelmatige tussenpozen de hoogte van de golf gemeten. Die hoogten zijn getallen, en op die manier kun je geluid voorstellen door een reeks van getallen.
|
| b. |
Hoe heet dat proces?
Sampling.
|
| c. |
Noem drie bestandsformaten waarin geluidsbestanden kunnen worden bewaard.
wav, mid, mp3
|
| d. |
Leg uit dat een niet-gecomprimeerd muziek-bestand van 1 minuut (44,1 kHz, 16 bits) ongeveer 10 MB geheugenruimte in beslag neemt.
44.1 kHz betekent dat er 44100 keer per sec. de hoogte van de geluidsgolf wordt gemeten. En 16 bits betekent dat elke hoogte wordt opgeslagen in 2 bytes.
Dat is dus 44100 × 2 bytes per seconde.
Per minuut is 60 × zoveel. En bij stereo-geluid komt het geluid via twee kanalen binnen en dan is het nog eens 2 × zoveel.
Totaal kom je dan op 44100 × 2 × 60 × 2 = 10.584.000 bytes per minuut, en dat is dus iets meer dan 10 Mb
|
| e. |
Als je een wav-bestand omzet in een MP3-bestand, hoeveel keer zo klein zal dat bestand dan ongeveer zijn?
12 keer zo klein
|
| f. |
Wat betekent: er is gesampled op 44,1 kHz?
Dat er 44100 keer per sec. de hoogte van de geluidsgolf wordt gemeten.
|
| g. |
Als je een wav-bestand hebt en je zet dat om in een mp3-file, en daarna zet je die mp3-file weer om in een wav-file, krijg je dan het oorspronkelijke bestand weer terug ? Waarom wel of niet?
Nee, omdat bij het omzetten naar een mp3-bestand alles wat niet voor het oor hoorbaar is uit het oorspronkelijke signaal wordt weggelaten. En wat is weggelaten kun je niet terugkrijgen.
|
|
|











