Binaire getallen
Hoe zit het nu precies met binaire getallen? Binaire getallen werken anders dan de getallen waar wij in het dagelijks leven mee werken. Getallen die we in het dagelijks leven gebruiken noemen we decimale getallen.
In het decimale stelsel kennen we 10 cijfers (0 t/m 9). In het binaire getallenstelsel kennen we maar 2 cijfers (0 en 1). Dit is een getallenstelsel dat voor ons heel handig is. Dat komt omdat een computer maar met twee signalen kan werken: hoog en laag. De 0 komt overeen met een laag signaal en de 1 met een hoog signaal.
Neem nu het getal 6453 uit het decimale stelsel. Het getal kent 4 cijfers. De 6 geeft het aantal duizendtallen aan, de 4 het aantal honderdtallen, de 5 het aantal tientallen en de 3 de rest.

Oftewel

Het getal is dus 6*103 + 4*102 + 5*101 + 3*100 = 6000 + 400 + 50 + 3 = 6453.
Voor getallen die ook tienduizendtallen bevatten komt er natuurlijk een kolom voor met 104. Bij honderdduizendtallen komt daar wéér een kolom voor maar dan met 105 etc.
In het binaire stelsel kennen we een soortgelijke opbouw.
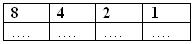
Oftewel

Omdat we in het binaire stelsel slechts 2 cijfers kennen (0 en 1) kunnen we op de puntjes ook alleen een 0 of een 1 invullen. Zoals je ziet werken we bij binaire getallen met machten van 2 omdat er maar 2 cijfers zijn (0 en 1). In het decimale stelsel werkten we met machten van 10 omdat we toen ook met 10 verschillende cijfers werkten (0 t/m 9).
Nemen we nu het binaire getal 1001 dan is dit dus:
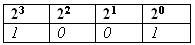
Dit is dus 1*23 + 0*22 + 0*20 + 1*20 = 8 + 0 + 0 + 1 = 9
We kunnen dit ook korter opschrijven door alleen de machten van 2 op te schrijven waar een 1 bij staat:
23 + 20 = 8 + 1 = 9
Dus het binaire getal 1001 is gelijk aan het decimale getal 9.
Opdracht 2
a.
Welk decimaal getal is gelijk aan het binair getal 1111?
b.
Welk decimaal getal is gelijk aan het binair getal 1011?
c.
Welk decimaal getal is gelijk aan het binair getal 0101?
klik hier voor de antwoorden, maar probeer het wel eerst zelf!
Omgekeerd kunnen we ook decimale getallen omrekenen naar binaire getallen. Dit is wel wat lastiger. We nemen als voorbeeld het decimale getal 39.
We kijken eerst naar welke grootste macht van 2 in 39 past. Dat is 25 (=32).
In de tabel hieronder komt dus bij 25 een 1 te staan. 39-32=7. we houden nu dus het restgetal 7 over.
We kijken weer naar welke grootste macht van 2 nu in 7 past. Dat is 22 (=4). Bij 22 komt dus ook een 1 te staan.
7-4=3. De grootste macht van 2 in het restgetal 3 is 21 (=2). 3-2=1. Er komt een 1 te staan bij 21.
Nu houden we dus nog het restgetal 1 over. Daar past nog maar één macht van 2 in en dat is 20 (=1). 1-1=0. Ook bij 20 komt een 1 te staan. We houden geen restgetal over. De overige machten van 2 waar we geen 1 in hebben gevuld zijn automatisch een nul.
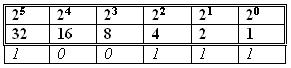
We hebben nu het binaire getal te pakken: 100111. Dit is dus gelijk aan het decimale getal 39. Controleer dit zelf door dit binaire getal om te schrijven naar een decimaal getal!
Als je de berekening hierboven moeilijk te volgen vond, dan kun je in de afbeelding hieronder kijken hoe deze stap voor stap is uitgevoerd.
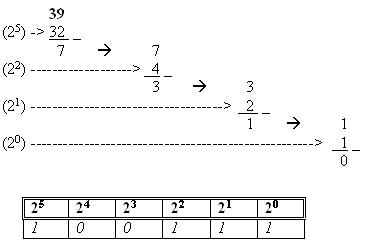
In het plaatje hierboven zie je linksbovenin het decimale getal 39 dat we naar een binair getal willen omschrijven. De hoogste macht van 2 die in 39 past is 25. Dat is gelijk aan 32. Je ziet dat er 32 van 39 gehaald wordt.
Het restgetal is 7 en daarvoor herhalen we de bewerking weer. Links houden we bij welke machten van 2 we steeds van het restgetal hebben gehaald. Vervolgens vullen we voor die machten van 2 een 1 in de tabel in. De rest is automatisch een 0.
Opdracht 2
d.
Welk binair getal is gelijk aan het decimaal getal 567?
e.
Welk decimaal getal is gelijk aan het binair getal 10011010?
f.
Welk binair getal is gelijk aan het decimaal getal 121?
g.
Welk decimaal getal is gelijk aan het binair getal 10011?
Klik hier voor de antwoorden, maar probeer het wel eerst zelf!






