PO over een aantal beroemde wiskundige problemen
Je gaat in deze PO een paar beroemde problemen die met kansberekening te maken hebben
bekijken
en proberen op te lossen.
HET DRIEDEUREN PROBLEEM
Het drie-deurenprobleem is een beroemd probleem dat nog niet zo heel erg oud is.
Het probleem staat ook wel
bekend als het 'Willem Ruis probleem' of 'The Monty Hall problem'.
Op internet is veel te vinden over het probleem.
Het probleem staat ook in je boek beschreven (wiskunde A1/B1 deel 2 blz. 171)
HET PROBLEEM
Stel je voor: je bent gast in een
spelshow. Voor je zie je drie deuren, maar achter slechts één
ervan ligt een prijs. Jij kiest één van de drie deuren, maar die
blijft nog gesloten. Nu komt
het: de quizmaster opent één van de twee andere deuren en laat je
zien dat daarachter de prijs niet ligt (dat kan hij doen omdat hij weet achter
welke deur de prijs ligt)
Nu krijg jij de kans alsnog te
wisselen, dus voor die andere dichte deur te kiezen. Je kunt ook
bij je keuze blijven, de deur van je eerste keus.
Wat doe je:
wissel je of wissel je niet?
GESCHIEDENIS
Dit is een probleem dat onder veel namen
bekend staat. De eerste versie ervan komt uit 1959 en werd
geformuleerd door Martin Gardner, bekend om zijn puzzels in de
'Scientific American'. Hij noemde het probleem: het dilemma van de
drie gevangenen.
In het begin van de jaren negentig bracht het
probleem de Amerikaanse media in beroering. Het staat daar bekend
onder de naam 'The Monty Hall Problem', vernoemd naar de
presentator van de televisieshow 'Let's make a deal'.
Ook in
Nederland haalt het probleem regelmatig de krant en ontstaat er
een geweldige discussie. Hier noemt men het probleem ook wel het
'Willem Ruis probleem', omdat Willem Ruis (een quizmaster uit de tachtiger jaren) het
toepaste in zijn show.
SIMULATIE
Je kunt het probleem simuleren met onderstaand applet (dat is een programma op een site).
Je kunt dan heel mooi zien wat het gevolg is van wisselen of juist bij je
oorspronkelijke keus blijven.
De applet werkt als volgt:
Jij kiest een deur door op het rondje eronder te klikken, en de applet verklapt je of achter
de gekozen deur wel of
geen prijs staat.
Bovendien vertelt de applet je welke deur door
de quizmaster is geopend.
Dat betekent dat je direct kunt nagaan
of je met niet wisselen of juist met wel wisselen de prijs hebt
gewonnen.
In het onderste tabelletje wordt bijgehouden hoe vaak je gewonnen zou hebben in elk
van de beide gevallen.
Opdrachten bij het driedeuren-probleem
- Ga op zoek naar de achtergrond van het
probleem; hetzelfde principe komt ook voor bij dilemma van de
drie gevangenen ? Beschrijf dat probleem.
- Simuleer het probleem heel vaak met het applet hierboven (minstens 50 keer)
Beschrijf wat je uitkomsten zijn.
- Probeer uiteindelijk een goed onderbouwde uitleg te geven waarom het wel of niet
wisselen gunstiger is.
Geef de kans op het winnen van een prijs als je niet wisselt, en ook als je wel wisselt, met een
berekening.
Het handelsreizigersprobleem
Een bekend probleem voor een
transportfirma: je hebt een aantal steden
die bezocht moeten worden door een vrachtwagen.
Alle steden moeten één keer bezocht worden en vervolgens kan de
vrachtwagen weer terug naar het bedrijf.
Tussen elk tweetal steden zit een bepaalde afstand en het probleem voor het bedrijf is om de
kortste route te
vinden.
Er zijn bepaalde oplossingsmethoden (algoritmen) om dit soort problemen snel op te lossen.
HET PROBLEEM VERKENNEN
We gaan het probleem wat vereenvoudigen.
We gaan er van uit dat een vrachtwagen naar één bepaalde plaats moet, maar dat hij uit een
heleboel routes kan kiezen.
En nu moet er eigenlijk worden uitgezocht wat de kortste route is, maar we beginnen met na te gaan hoeveel
routes er zijn
en hoeveel rekentijd het kost om alle mogelijke routes te onderzoeken.
Stel je hebt een route met 3 steden, A, B, en C. Tussen elk tweetal steden loopt e´´n weg.
En hij moet van A naar C.
Dan kan hij rechtstreeks van A naar C, maar hij kan ook via B, dus route ABC en misschien is die wel
korter. Dan kan hij dus uit 2 routes kiezen.
Vervolgens kun je berekenen uit hoeveel routes hij kan kiezen bij 4 steden, dan bij 5 steden enz.
We nemen aan dat alle steden rechtstreeks met elkaar verbonden zijn.
Stel dat je dan per onderzochte route een duizendste seconde rekent (immers, een pc kan zo'n berekening
van de
totale afstand van een route snel uitvoeren). Dan kun je een tabel maken voor n=3 tot en met
n=20 steden met de daarbij horende totale rekentijd.
Behalve dit recht-toe-recht-aan (na´eve) algoritme zijn er snellere
oplossingsmethoden te vinden. Eén daarvan is ontworpen door de Nederlandse
programmeur Dijkstra in de periode vlak na de oorlog.
Hieronder vindt je een applet. Met behulp hiervan kun je een beschrijving maken van de stappen die
Dijkstra's algoritme achtereenvolgens doorloopt voordat deze een oplossing heeft gevonden.
Een voorbeeld waarbij het gebruikt wordt is de routeplanner van de NS.
Het kortste pad volgens Dijkstra
Als je op Example klikt, en steeds op step dan zie je hoe de kortste routes worden bepaald.
Je kunt ook zelf een tekening maken. Klik waar je een knooppunt wilt hebben, sleep
wegen tussen knooppunten waar je die wilt hebben.
Het applet neemt aan dat je met éénrichtingswegen werkt, zijn beide richtingen toegestaan
dan moet je in beide richtingen een weg slepen.
De lengte van een weg kun je laten varieren van 0 t/m 100 km. door het pijltje te verslepen.
Opdrachten bij het handelsreizigersprobleem
- Geef een tabel met het aantal routes, de rekentijden voor
het narekenen van alle
mogelijke routes in sec. en ook in uren, van 3 tot en met 20 steden bij de na´eve methode.
Doe dat met behulp van Excel.
- Probeer door middel van het applet uit te vinden welke stappen achtereenvolgens in
Dijkstra's algoritme worden genomen. Geef een beschrijving en uitleg.
Doe dat aan de hand van de volgende figuur, waarbij de kortste route van a naar g moet
worden bepaald. Leg dus uit hoe je m.b.v. het Dijkstra-algoritme die kortste afstand kunt bepalen.
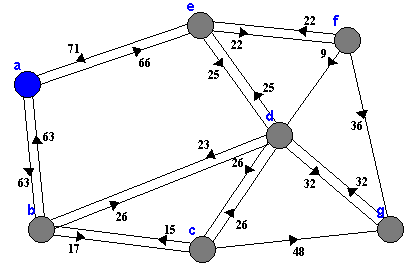
- Is het een snel algoritme om de kortste route te vinden? Vergelijk de
efficiŰntie van de na´eve methode en Dijkstra's algoritme bij bovenstaand voorbeeld met 7 steden.
- Weet je nog andere terreinen waar Dijkstra's algoritme wordt toegepast ?
Praktische opdracht
Deze praktische opdracht moet je uitvoeren in groepjes van 2.
Je maakt er een schriftelijk verslag van.
- Het verslag bevat een voorblad waarop de namen van de leden van het groepje en de titel
van de opdracht.
- Dan de inhoudsopgave.
- Dan de uitwerking van de opdrachten. Je moet het zo beschrijven dat het ook te volgen is voor
iemand die het opdrachtenblad niet heeft.
- Verder moet je niet alleen de antwoorden opschrijven maar je moet ook uitleggen hoe je aan het
antwoord gekomen bent.
- Je voegt aan het verslag ook een logboek toe, daarin staat beschreven wie wat en wanneer gedaan heeft.
Dat kun je in de tabel hieronder bijhouden.
- Het verslag lever je ..................... persoonlijk bij me in.
- De beoordeling gaat via STIP :
- S =struktuur , T = techniek en taal, I = inhoud, P =presentatie en proces
|
Logboek PO WA vwo-5 van .......... en ................. |
|
datum |
tijd |
Werkzaamheden |
door |
opmerkingen |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|