PO Wiskunde, over beweegbare werktuigen: hijskranen, strijkplanken, busdeuren, tekenapparaten, enz.Werk de volgende opdrachten uit. Je moet het zo beschrijven dat het ook te volgen is voor iemand die het opdrachtenblad niet heeft.Verder moet je niet alleen de antwoorden opschrijven maar je moet ook uitleggen hoe je aan het antwoord gekomen bent. Gebruik illustraties en tekeningen om de antwoorden te verduidelijken. Verklaar de dingen zo helder mogelijk op een wiskundig verantwoorde manier. Bij sommige voorbeelden maak je gebruik van de computer. Bij de voorbeelden 9 en 10 is het de bedoeling met bewegende hijskranen op de computer te experimenteren. Bij opdracht 18 moet je ook gebruik maken van een applet op een site. Voorbeeld 1: Torenkraan Zulke reusachtige kranen zie je bij elk bouwwerk van enige omvang.  De horizontale hoofdarm boven op de toren kan draaien en blijft
steeds horizontaal.
De horizontale hoofdarm boven op de toren kan draaien en blijft
steeds horizontaal.
Langs de hoofdarm glijdt de loopkat; dus van de toren af of er naar toe. Onder de loopkat hangt de takel met de last, datgene wat de kraan moet verplaatsen. De last hangt aan de hijskabel. Door de hijskabel met de hijslier op of af te rollen, gaat de last omhoog of omlaag. Met deze drie bewegingen (draaien, loopkat verplaatsen en last omhoog of omlaag bewegen) kan de kraanmachinist de last ophalen en brengen waar nodig is. Hier links zie je wat details. De hijskabel is één doorlopend geheel. Hij zit vast aan het uiterste einde van de looparm, gaat via katrollen door de loopkat en de takel en komt boven de toren bij de hijslier, die hem kan opwinden en afrollen. Heel bijzonder is het volgende: als de hijslier op de rem staat, kan de loopkat nog wel langs de hoofdarm bewegen. Toch beweegt de last dan niet op of neer! 
Opdrachten Torenkraan
Voorbeeld 2: Antieke waterput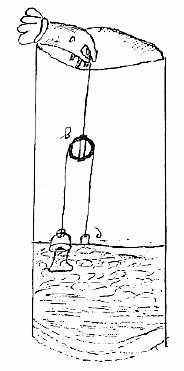 Je zult toch maar elk litertje water dat je gebruikt voor koken, wassen en drinken eigenhandig
met een emmer en een touw uit de put moeten halen. Toch was dat vroeger in Nederland heel
gewoon en is het in sommige streken van de wereld nog steeds zo...
Je zult toch maar elk litertje water dat je gebruikt voor koken, wassen en drinken eigenhandig
met een emmer en een touw uit de put moeten halen. Toch was dat vroeger in Nederland heel
gewoon en is het in sommige streken van de wereld nog steeds zo...
Putten kunnen diep zijn. In woestijngebieden is 60 meter heel gewoon en 25 meter in Nederland ook. Vandaar dat er slimme trucs bedacht zijn om met minder touw dan verwacht toch de diepte te 'overbruggen'. Isaac Beeckman maakt op 18 juli 1612 in zijn dagboek de volgende aantekening daarover met een tekening erbij. Een tikkeltje oud, zijn taal. Maar best te begrijpen.
Water putten
Jan Boom seyde, dat hy een kunste wist, die schier niemant meer en wiste ende was, dat hy eenen emmer waters op konde halen met half soveel touwe op te trecken als den put diep was ende en wilde dat my niet leeren. Opdrachten Waterput
Voorbeeld 3: De strijkplankHet raadsel van de strijkplank: verschillende hoogtes, maar altijd horizontaal!Hier twee standen, voor de grotere huisvrouw en kleinere huisman. En een blik onder de plank.  Opdracht Strijkplank

Voorbeeld 4: Een HoogwerkerIn alle standen is het blad van de strijkplank horizontaal.Bij omhoog brengen van het blad wordt het parallel verplaatst. Parallelverplaatsing is van groot belang bij hoogwerkers, dat is duidelijk. Het mechaniek van deze schaarhoogwerker moet dus ook parallelverplaatsing opleveren. Opdrachten Hoogwerker
Voorbeeld 5: Een Motorheftafel Garagehouders willen graag goede spullen om auto's
en motorfietsen omhoog te brengen, zodat repareren mogelijk wordt en de ruggen van de technici worden
gespaard. Garagehouders willen graag goede spullen om auto's
en motorfietsen omhoog te brengen, zodat repareren mogelijk wordt en de ruggen van de technici worden
gespaard.
Ook bij de hier afgebeelde motorheftafel is parallelverplaatsing aan de orde. Opdrachten Motorheftafel
Voorbeeld 6: De TreindeurenDe deuren van treinen en bussen worden met een betrekkelijk eenvoudig mechaniek bediend.De deur gaat naar buiten open en beschrijft daarbij een boog, waarbij de richting waarin de deur ligt eigenlijk nauwelijks verandert. Tot slot komt de deur weer dichter naar de wand van de bus of de trein, naast het deurgat. Twee stangen zorgen er voor dat dit lukt. Zie de foto's.  Opdrachten Treindeuren

Voorbeeld 7: De PantograafEen vergroter van punaises en karton!Deze Verdubbelaar kun je zelf met kartonnen stroken en punaises maken. In tekening: 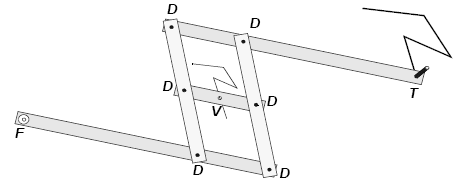 Bij F zit de punaise met de punt in de tafel, in ieder geval aan het tekenblad vast. Het is een geFixeerd punt. Bij de zes D's steken de punaises door twee stroken karton. Het zijn Draaipunten. Het punt bij V volgt de gegeven figuur die er onder te zien is. Bij T zit een potloodstift, met een klein extra gewichtje van twee eurostukken en een plakbandje. Dat is het Tekenpunt. Je kunt ook het tekenpunt T met de hand leiden, terwijl je naar V kijkt om V over de gegeven figuur te voeren. De figuur die door T getekend wordt, is een vergroting van de figuur waar V over loopt. Opdrachten Pantograaf
Voorbeeld 8: Stangenvierhoeken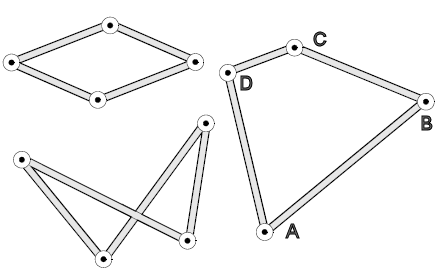 Stel je de hier getekende figuren voor als gemaakt van latjes of stangen en met scharnierende hoekpunten. Stel je de hier getekende figuren voor als gemaakt van latjes of stangen en met scharnierende hoekpunten.Dit weet je vast wel: Driehoeken zijn star maar de vierhoeken zijn beweeglijk. De technische term voor zo'n beweeglijke vierhoek is: stangenvierhoek . De stangenvierhoek van het volgende voorbeeld kun je goed met stroken en punaises maken. De vijf-drie-drie-drieVan vierhoek ABCD zijn A en B punten die op hun plaats blijven (gefixeerd). Alle punten zijnwel scharnierpunten. Verder geldt: AB = 25 cm, BC = CD = DA = 15 cm. Het is dus net zo'n vierhoek als de rechter vierhoek ABCD in de figuur hier boven, maar de lengten daar kloppen niet. Opdrachten vijf-drie-drie-drie-stangenvierhoek
Voorbeeld 9: De hijskraan op de computer.De gewoonste hijskraan die er is: zo'n rijdend wagentje met een arm.Die vind je als eerste van de twee hijskranen als je op applet voor twee hijskranen klikt.  Bediening: Bediening:
Je kunt de rode stippen verslepen. Er staat bij wat het effect is, maar dat kun je ook wel direct zien:
Als je van deze kraan de hijslier stil zet en de kraanarm beweegt, zal de last niet op dezelfde hoogte blijven, zoals dat bij de torenkraan het geval was. In de terminologie die we bij de torenkraan leerden: De gewone kraan heeft geen exact horizontale lastweg. Toch is het mogelijk een flink stuk (bijna) horizontale lastweg te creëren. Let wel: bij het draaien van de arm blijft de last dan dus redelijk op dezelfde hoogte. Daartoe moet het rolpunt bovenin goed gekozen worden. Dat is dan ook verplaatsbaar. Opdrachten gewone hijskraan
Voorbeeld 10: Kraan met vertikaal geleide arm Er zijn ook kranen met een vertikaal geleide arm.
Er zijn ook kranen met een vertikaal geleide arm.
Het linkereind van de kraanarm kan dan vertikaal op en neer kan bewegen. Bij zo'n kraan is wel sprake van een horizontale lastweg. We gaan nu onderzoeken hoe dat zit. Een bewegend model van de kraan kun je net zo krijgen als bij voorbeeld 9: Je vindt hem als tweede van de twee hijskranen als je op applet voor twee hijskranen klikt. Bij deze kraan is AD vertikaal. A is een vast draaipunt. BE is de kraanarm. C is een vast scharnierpunt op BE. B kan op en neer worden bewogen. Daardoor kan de kraanarm BE dus bewegen. Gegeven is: AC = BC. Er wordt dus steeds voor gezorgd dat AC even lang is als BC. De hijskabel loopt via de route DBCEL. Opdrachten kraan met vertikaal geleide arm
Praktische opdrachtDeze praktische opdracht moet je uitvoeren in groepjes van 2.Je maakt er een schriftelijk verslag van.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

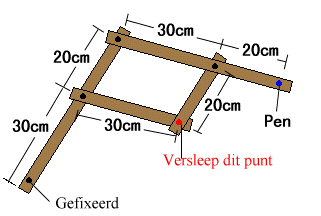 Een ander model van een pantograaf zie je hier rechts.
Een ander model van een pantograaf zie je hier rechts.

 Onderzoek hoe je het rolpunt moet plaatsen om een zo goed mogelijke horizontale lastweg
te krijgen, en geef aan waar die plaats is.
Onderzoek hoe je het rolpunt moet plaatsen om een zo goed mogelijke horizontale lastweg
te krijgen, en geef aan waar die plaats is.