PO WB over een aantal bekende wiskundige problemen
Je gaat in deze PO een paar bekende problemen, die met integralen en bogen in cirkels te maken hebben,
bekijken en proberen op te lossen.
A. De kans op twee oplossingen bij een kwadratische vergelijking
PROBLEEMOMSCHRIJVING
De kwadratische
vergelijking x2 + bx + c = 0 kan nul, één of twee oplossingen
hebben.
Als je voor b en c willekeurige getallen kiest die bijvoorbeeld tussen -100 en 100 liggen
dan zijn de kansen op nul, één of twee oplossingen niet
gelijk.
De kans op géén oplossingen is kleiner dan de kans op
twee oplossingen.
Je gaat nu uitzoeken hoe dat precies zit.
Dat kan met behulp van een integraal.
Je kunt het eerst proefondervindelijk uitzoeken.
Pak je grafische rekenmachine (=GRM) er bij. Daar kun je random-getallen (dat zijn willekeurige getallen)
mee genereren.
Als je randInt(-100,100) invoert dan geeft de rekenmachine een willekeurig geheel getal
tussen -100 en 100
(randInt krijg je op je GRM door op MATH te drukken, dan zet je de cursor op PRB en dan kies
je nummer 5).
Bij mij verscheen er 72, dat noem ik b
Als je dan op enter drukt wordt de laatste opdracht herhaald, dan krijg je weer
een willekeurig getal.
Bij mij verscheen er 34, dat noem ik c
Dan bereken je de discriminant D = b2-4ac , dat werd bij mij
72 x 72 - 4 x 34 = 5048
(denk er om: de vergelijking is
x2 + bx + c = 0 en dus geldt a=1)
en dat betekent dat er twee oplossingen zijn.
Zo kun je doorgaan, steeds twee willekeurige getallen genereren en kijken of er twee oplossingen zijn
of niet. Als je dat 100 keer doet krijg je wel een idee hoe die kansen liggen.
Maar dan ben je wel even bezig. En het kan veel sneller, als je er een programma voor hebt op je GRM.
Dat programma kun je zelf invoeren op de volgende manier:
Druk op PRGM, zet dan de cursor op NEW en druk op ENTER
Er verschijnt : Name= en de cursor staat in de vorm van een A te knipperen.
Je moet dan de naam van het programma invoeren.
Tik in: PO, dan enter
(de P staat boven de 8, de O boven de 7. Druk die toetsen in, want
de GRM staat al op letters ingesteld, dat zie je aan de knipperende A )
En dan kun je het programma invoeren.
Elke opdracht komt op een nieuwe regel.
Als je een letter moet hebben dan druk je eerst op ALPHA en dan op de toets waar de groene letter boven
staat.
Druk je op 2ND en dan op ALPHA dan blijft de GRM op letters ingestelt tot je dat opheft door weer op
ALPHA te drukken.
Sommige opdrachtwoorden moet je niet gewoon intypen, maar die krijg je op een andere manier.
Dat zijn de woorden die cursief zijn afgedrukt.
Hoe je die krijgt lees je onder het programma.
PROGRAM PO
: ClrHome
: 0 → L
: FOR (I,1,100)
: randInt(-100,100) → B
: randInt(-100,100) → C
: B2-4C → D
: IF D>0
: THEN
: L+1→L
: END
: END
: DISP "AANTAL VAN DE 100 MET D>0:",L
-
ClrHome krijg je door op PRGM te drukken, dan moet je de cursor op I/O zetten en dan Clrhome uitkiezen.
- → krijg je door op STO te drukken.
- FOR krijg je door op PRGM te drukken, en dan is de vierde mogelijkheid FOR
- randInt krijg je door op MATH te drukken, dan moet je de cursor op PRB zetten en dan randInt
uitkiezen.
- IF krijg je door op PRGM te drukken, en dan is de eerste mogelijkheid IF
- > krijg je door op TEST te drukken, en dan > uit te kiezen
- THEN krijg je door op PRGM te drukken, en dan is de tweede mogelijkheid THEN
- END krijg je door op PRGM te drukken, en dan is de zevende mogelijkheid END
- DISP krijg je door op PRGM te drukken, dan moet je de cursor op I/O zetten en dan DISP uitkiezen.
Opdrachten bij de kans op twee oplossingen
- Voer bovenstaand programma in op je GRM.
Laat het programma vijf keer lopen en noteer de uitkomsten.
(Het duurt op mijn rekenmachine 13 sec. voordat de oplossing verschijnt, je moet dus wel even geduld
hebben !)
Wat volgt hier uit voor de kans op twee oplossingen, als je gehele getallen tussen -100 en 100
voor b en c neemt ?
- We hebben tot nu toe steeds gehele getallen voor b en c genomen.
We nemen nu aan dat b en c kommagetallen tussen -1 en 1 zijn.
En we kijken weer hoeveel oplossingen de vergelijking dan heeft.
Je kunt met je GRM ook willekeurige komma-getallen genereren.
Dat doe je met rand (Druk op MATH, ga naar PRB en kies voor rand).
Dat levert een kommagetal tussen 0 en 1
Als je 2 * rand invoert krijg je een kommagetal tussen 0 en 2
Als je 2 * rand - 1 invoert krijg je een kommagetal tussen -1 en 1 en dat is de bedoeling
Verander bovenstaand programma zo dat je
: randInt(-100,100) → B
verandert in
: rand*2-1 → B
en
: randInt(-100,100) → C
verander je in
: rand*2-1 → C
(Als je het programma wilt veranderen moet je op PRGM drukken, dan moet je de cursor op EDIT en op PO
zetten en op enter drukken)
Laat het veranderde programma vijf keer lopen en noteer de uitkomsten.
Wat volgt hier uit voor de kans op twee oplossingen, als je komma-getallen tussen -1 en 1 voor
b en c neemt ?
- Als je voor b en c willekeurige getallen kiest uit het interval [-1 , 1] dan kun je de kans
op twee oplossingen met behulp van een integraal uitrekenen.
Als er geen oplossing is, dan moet gelden:
b2 - 4ac < 0 dus b2 - 4c < 0 (want a = 1)
Dus moet er gelden: c > b2 / 4
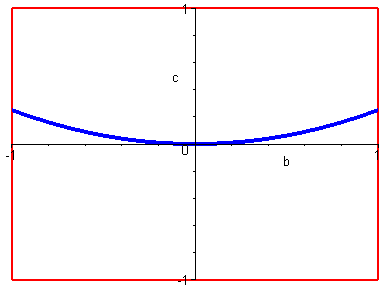 In de figuur hiernaast is de grafiek van c = b2 / 4
getekend
In de figuur hiernaast is de grafiek van c = b2 / 4
getekend
Als je voor b en c willekeurige getallen kiest uit het interval [-1 , 1] dan stelt (b,c) een punt in de
figuur voor waarvan b en c de coöordinaten zijn.
Als het punt op de parabool ligt dan geldt: c = b2 / 4
Als het punt boven de parabool ligt dan geldt: c>b2/4
En als het punt onder de parabool ligt dan geldt: c < b2 / 4
In dit kansprobleem zijn kansen verhoudingen van oppervlakten.
De kans op geen oplossing is de verhouding van de oppervlakte boven de grafiek en de
totale oppervlakte.
Met een integraal kun je dus de precieze kans op geen oplossing berekenen.
De totale oppervlakte hoort bij de totale kansruimte ( = alle mogelijke uitkomsten) en is in dit geval
gelijk aan de oppervlakte van het vierkant = 2*2 = 4.
Laat (met behulp van een integraal) zien dat de kans op geen oplossing in het
bovenstaande probleem exact gelijk is aan 11/24 (dus geen benadering met kommagetallen!)
-
Ga weer uit van de kwadratische vergelijking x2 + bx + c = 0.
Maar neem deze keer voor b en c willekeurige komma-getallen tussen -2 en 2
Benader eerst experimenteel de kans op twee oplossingen.
En bereken daarna de exacte kans op twee oplossingen met behulp van een integraal.
- Neem nu voor b en c willekeurige komma-getallen tussen -100 en 100
Benader weer experimenteel de kans op twee oplossingen.
Maakt het veel verschil of je gehele getallen tussen -100 en 100 neemt of kommagetallen ?
En bereken ook weer de exacte kans op twee oplossingen met behulp van een integraal.
- Wat wordt de kans op twee oplossingen als je voor b en c elk willekeurige
getal mag nemen, dus als er geen grenzen voor b en c zijn ?
Probeer dat te beredeneren.
- Bepaal de kans dat de derdegraadsvergelijking
x3 -3bx + 2c = 0 drie oplossingen heeft als b en c
willekeurige kommagetallen tussen 0 en 2 zijn
Aanwijzing:
schets eerst de grafieken van een
paar mogelijke functies.
Bereken met behulp van de afgeleide functie de waarden van x (uitgedrukt in a) waarvoor er een maximum
en/of een minimum is.
Vul die waarden in de functie in, dan krijg je de waarde van het maximum en van het minimum
(uitgedrukt in a en b)
Als het maximum positief is en het minimum negatief dan zijn er drie snijpunten met de x-as.
Je kunt dan net zoals hierboven m.b.v. een integraal de gevraagde kans berekenen.
B. Het lucifer-probleem
Als je een lucifer op een blad papier gooit waarop evenwijdige lijnen getekend zijn dan kan de
lucifer over een lijn heenvallen of niet.
De kans dat de lucifer op een lijn valt is afhankelijk van de afmetingen van de lucifer en van de
constante
afstand tussen de lijnen.
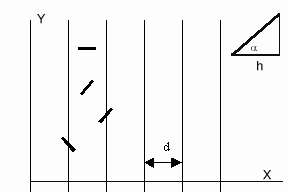
Hieronder zie je een situatieschets met een
aantal standen van de lucifer. Je ziet dat twee lucifers tussen de lijnen in zijn gevallen en twee
zijn op een lijn gevallen. (het gaat om de vertikale lijnen, de horizontale lijn is er alleen
bijgetekend voor het coördinatenstelsel, dat is de x-as)
Voor het gemak wordt de lucifer opgevat als
een lijnstuk met lengte 1, de dikte verwaarlozen we.
HET PROBLEEM
We willen weten wat de kans is dat de lucifer niet over een
lijn valt als d = 2 ( dat betekent dat de afstand tussen de lijnen twee keer zo groot is
als de lengte van een lucifer.
Ook bij dit probleem kom je weer een integraal tegen, en het antwoord blijkt iets
met p te maken te hebben.
We gaan het probleem eerst weer proberen proefondervindelijk op te lossen, en daarna theoretisch.
Je kunt het proefondervindelijk uitzoeken door een paar lijnen op een stuk papier te tekenen, en
wel zo dat de afstand tussen die lijnen twee keer zo groot is als de lengte van een lucifer.
En dan laat je bijvoorbeeld 100 keer een lucifer op het blaadje vallen, en je telt hoevaak de lucifer
over een lijn heen valt.
Maar dat is een heel gedoe, en daarom is het waarschijnlijk handiger om het weer te simuleren met
de GRM.
Hoe kun je de plaats van een gevallen lucifer simuleren met de GRM ?
Voor die plaats is de x-coördinaat van het linker eindpunt van de lucifer belangrijk, die geven
we aan met x. En de hoek waaronder hij is gevallen, de hoek met een horizontale
lijn geven we aan met a (zie de rechter bovenhoek van de figuur).
De y-coördinaat is niet belangrijk.
Als je 5 vertikale lijnen hebt, dan zit daar in totaal 10 cm. tussen. Dan kan de x variëren
van 0 tot 10. Op de GRM krijg je een willekeurig getal tussen 0 en 10 met rand*10
En de hoek kan variëren van 0 tot 90 graden. Op de GRM krijg je een willekeurig getal tussen 0 en 90
met rand*90
Dus x = rand*10
Toen ik dat probeerde op mijn GRM kreeg ik x=7.34
En a = rand*90
Toen ik dat probeerde op mijn GRM kreeg ik a = 32.40
Als ik dan wil vaststellen of de lucifer in die stand over een vertikale lijn valt dan moet ik eerst
de horizontale projectie van de lucifer berekenen (dat geef ik aan met h, zie figuur)
Er geldt h = cos 32.40° = 0.84
Dan is de x-coördinaat van het eindpunt 7.34 + 0.84 = 8.18 , en dus valt de lucifer over de lijn
die op x=8 staat.
Als x=1.34 en a = 32.40 dan krijg je net zo'n berekening, en dan krijg
je 1.34 + 0.84 = 2.18 en dus valt die lucifer over de lijn die op x=2 staat.
Dat heeft tot gevolg dat je voor x ook wel een willekeurig getal tussen 0 en 2 kunt nemen !
Zo kun je doorgaan, steeds twee willekeurige getallen genereren: x=rand*2 en
a=rand*90, en dan x + cos a° berekenen.
Als dat groter dan 2 is betekent het dat de lucifer over de lijn gevallen is.
Als je dat 100 keer doet krijg je wel een idee hoe die kansen liggen.
Maar het is weer veel handiger er even een programma voor te maken op je GRM.
Voer dat programma als volgt in:
PROGRAM PO
: ClrHome
: 0 → L
: FOR (I,1,100)
: rand*2 → X
: rand*90 → A
: cos(A) → H
: IF X+H>2
: THEN
: L+1→L
: END
: END
: DISP "AANTAL VAN DE 100 OVER DE LIJN:",L
Opdrachten bij het lucifer-probleem
-
Voer bovenstaand programma in op je GRM.
Laat het programma vijf keer lopen en noteer de uitkomsten.
Wat volgt hier uit voor de kans op het vallen over een lijn ?
- Nu theoretisch.
- Stel je voor dat je 100 lucifers laat vallen, en dat die allemaal evenwijdig aan de x-as
blijven liggen, regelmatig verdeeld over de xas. We mogen ons beperken tot x-waarden tussen 0 en 2 hebben
we hierboven gezien.
Als de x-waarden regelmatig zijn verdeeld dan geldt voor die x-waarden
bijvoorbeeld: x=0, x=0.02, x=0.04, x=0.06 enz. t/m x=1.98
Dan zijn 50 lucifers tussen de lijnen, en 50 er over gevallen.
- Als je nog eens 100 lucifers laat vallen en die vallen allemaal onder een hoek van bijv.
40°, en de x-waarden zijn weer regelmatig verdeeld, dan geldt voor die
x-waarden weer: x=0, x=0.02, x=0.04, x=0.06 enz. t/m x=1.98
cos 40°=0.776 , dat betekent dat de lucifers vanaf x = 1.24 allemaal over
een lijn vallen en de rest niet.
Dus 62 niet (dat is 124/2) en 38 wel (dat is 77.6/2 en dan afgerond, dus
100*(cos 40°)/2)
- Als je nu 9000 lucifers laat vallen en die vallen zo dat de hoek en de x regelmatig is
verdeeld, dan zijn er 100 onder een hoek van 0°,
met x=0, x=0.02, x=0.04 enz., er zijn ook 100 onder een hoek van 1°,
met x=0, x=0.02, x=0.04 enz., en er zijn 100 onder een hoek van 2°,
met x=0, x=0.02, x=0.04 enz., enz.
- Als je dan wilt weten hoeveel van die 9000 er over een lijn zijn gevallen dan moet je o.a de
volgende optelling maken:
cos 0° + cos 1° +
cos 2° + enz.
Dat kan op de GRM met sum(seq(.......))
Hoeveel wordt dat, en hoe groot is de kans dus ?
- De vorige berekening is een benadering. De hoeken zijn natuurlijk nooit precies
0°, 1° enz.
De berekening met sum(seq(...)) is eigenlijk de ondersom, en het exacte antwoord krijg je met een
integraal.
Hoe gaat dat precies ? En wat komt er dan uit die kans ? Komt het getal π er
ook in voor als je het
exact berekent?
C. De baan van het middelpunt van de ingeschreven cirkel
Opdrachten bij het bepalen van de baan van het middelpunt van de ingeschreven cirkel
-
Teken m.b.v. GeoGebra een cirkel met middelpunt M
Teken verder driehoek ABC, waarvan de hoekpunten op de cirkel liggen.
Construeer het middelpunt I van de ingeschreven cirkel van driehoek ABC, en teken die cirkel.
Leg uit hoe je dat middelpunt en die cirkel tekent
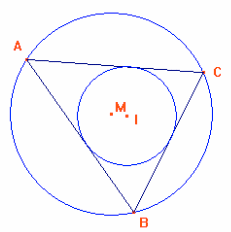
- Klik met de rechter muisknop op punt I, en zet het Spoor aan.
Beweeg nu punt C over de eerste cirkel. Welke vorm doorloopt het punt I dan?
Sla de tekening op als opdracht_C. Dat bestand moet je ook inleveren.
-
Bewijs dat ∠ AIB = 90° - ½ ∠ C
-
Bewijs dat punt I een gedeelte van een cirkel doorloopt.
-
Geef aan waar het middelpunt van die cirkel ligt.
D. Het spiegelbeeld van het hoogtepunt in een zijde
Opdrachten bij het bepalen van het spiegelbeeld van het hoogtepunt in een zijde
-
Teken m.b.v. GeoGebra een cirkel met middelpunt M
Teken verder driehoek ABC, waarvan de hoekpunten op de cirkel liggen.
Teken ook de hoogtelijnen uit A en uit B. Geef het snijpunt van de hoogtelijnen aan met H, dat wordt het hoogtepunt genoemd.
Het snijpunt van de hoogtelijn uit A met BC geven we aan met Ha (in GeoGebra mag je het wel met een andere letter
aangeven).
Het snijpunt van de hoogtelijn uit A met de omgeschreven cirkel geven we aan met Ha' (in GeoGebra mag je ook
dit punt wel met een andere letter aangeven).
Het snijpunt van de hoogtelijn uit B met AC geven we aan met Hb.
Laat GeoGebra de afstand van H tot Ha meten, en ook de afstand van Ha tot Ha'
Wat merk je op?
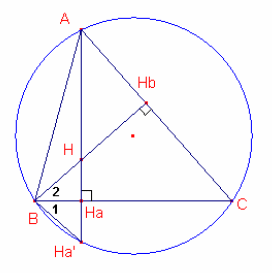
- Beweeg nu punt C over de cirkel. Wat merk je op over de afstanden HHa en HaHa' ?
Sla de tekening op als opdracht_D. Dat bestand moet je ook inleveren.
-
Bewijs dat de afstanden HHa en HaHa' gelijk zijn.
Aanwijzing:
Aan welke hoek zijn ∠B1 en ∠B2 allebei gelijk? Wat betekent dat voor ∠B1 en ∠B2?
Welke congruente driehoeken zie je dan?
E. De voetpunten van een punt t.o.v. een driehoek op een rechte lijn
Opdrachten bij het bepalen van de voetpunten van een punt t.o.v. een driehoek
-
Teken op een nieuw werkblad in GeoGebra drie punten A, B, C. Teken ook de lijnen AB, BC en CA.
Teken nu een punt P, kies het punt P om te beginnen binnen driehoek ABC.
Teken de loodlijnen uit P op BC (snijpunt A'), op CA (snijpunt B') en op AB (snijpunt C').
Teken vervolgens driehoek A'B'C'.
figuur E1
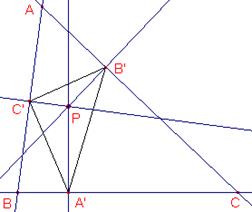
Driehoek A'B'C' heet de voetpuntsdriehoek van het punt P ten opzichte van driehoek ABC.
De hoekpunten van de driehoek heten de voetpunten van P ten opzichte van driehoek ABC.
Beweeg punt P in verschillende richtingen, binnen en buiten de driehoek.
Er zijn posities van het punt P waarvoor de drie zijden van driehoek A'B'C' op een rechte lijn liggen.
Welke posities van P zijn dat? Geef een beschrijving van je bevindingen.
-
Ga verder met de bij opdracht 16 gemaakte tekening.
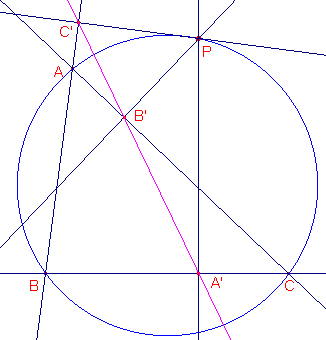
Construeer de omgeschreven cirkel van driehoek ABC.
Verplaats punt P binnen, op en buiten de cirkel.
Geef een beschrijving van je bevindingen met betrekking tot de voetpuntsdriehoek van het punt P
ten opzichte van driehoek ABC.
Sla de tekening op als opdracht_D. Dat bestand moet je ook inleveren.
Je hebt waarschijnlijk al een vermoeden dat de volgende stelling geldt:
De voetpunten van een punt dat gelegen is op de omgeschreven cirkel van een driehoek liggen op een rechte lijn.
Deze stelling moet je bewijzen, en we helpen je daarbij een eind op weg.
Als je deze stelling wilt bewijzen dan moet je dus aantonen dat A', B' en C' op één lijn liggen.
Maar hoe bewijs je dat drie punten op één lijn liggen, anders gezegd: hoe bewijs je dat drie punten collineair zijn?
Je kunt dat doen door aan te tonen dat ∠ A'B'C' = 180°
- Maar om aan te tonen dat A', B' en C' collineair zijn, kun je ook bewijzen dat ∠ AB'C' =
∠ CB'A'. Leg dat uit.
figuur E2
- De vierhoeken AB'PC' en CPB'A' zijn koordenvierhoeken. Geef hiervoor een bewijs.
(TIP: Maak gebruik van de omgekeerde koordenvierhoekstelling en opgave 19 op bladzijde 163 van
Wiskunde B deel 2 van Moderne Wiskunde)
In figuur E3 hebben we nog twee lijnstukken, PA en PC, en twee cirkels toegevoegd.
Immers als je een koordenvierhoek hebt past er een cirkel omheen.
figuur E3
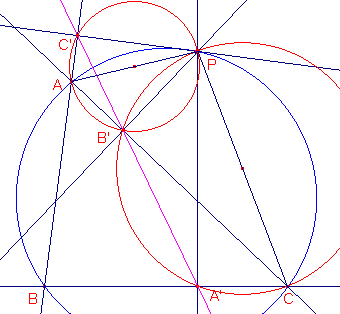
- In figuur E3 zijn nog twee andere koordenvierhoeken aan te wijzen.
Welke zijn dat?
figuur E4
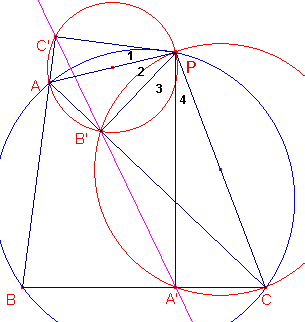
In figuur E4 zijn de vier hoeken bij P genummerd. De hoeken van driehoek ABC geven we opvolgend aan
met a, b en g.
- Nu geldt:
P1 + P2 + P3 + b = 180 °
en
P2 + P3 + P4 + b = 180 °
Leg dit uit. Wat zegt dit over P1 en P4?
- Aan welke hoek in CPB'A' is P4 gelijk? Waarom?
Aan welke hoek in AB'PC' is P1 gelijk? Waarom?
Waarom zijn de punten A', B', C' nu collineair?
Werkwijze bij deze praktische opdracht
Deze praktische opdracht moet je uitvoeren in groepjes van 2.
Je maakt er een schriftelijk verslag van.
- Het verslag bevat een voorblad waarop de namen van de leden van het groepje en de titel
van de opdracht.
- Dan de inhoudsopgave.
- Dan de uitwerking van de opdrachten. Je moet het zo beschrijven dat het ook te volgen is voor
iemand die het opdrachtenblad niet heeft.
- Verder moet je niet alleen de antwoorden opschrijven maar je moet ook uitleggen hoe je aan het
antwoord gekomen bent.
- Je voegt aan het verslag ook een logboek toe, daarin staat beschreven wie wat en wanneer gedaan heeft.
Dat kun je in de tabel hieronder bijhouden.
- Het verslag lever je uiterlijk .............................. persoonlijk bij me in.
- De beoordeling gaat via STIP :
- S =struktuur , T = techniek en taal, I = inhoud, P =presentatie en proces
|
Logboek PO WB vwo-5 van ................. en ................. |
|
datum |
tijd |
Werkzaamheden |
door |
opmerkingen |
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|

 In de figuur hiernaast is de grafiek van c = b2 / 4
getekend
In de figuur hiernaast is de grafiek van c = b2 / 4
getekend




