Hoofdstuk 17: Beveiliging en Cryptografie
 17.1. Inleiding
17.1. Inleiding
Als je een computer gebruikt heb je met verschillende soorten beveiligingen te maken.
Om je te beveiligen tegen virussen, hackers en/of spyware heb je een virusscanner en een firewall nodig.
Als je een draadloos netwerk gebruikt moet je er voor zorgen dat het netwerk beveiligd is, zodat niet iedereen er zomaar gebruik
van kan maken.
Als je iets bestelt bij een online boekhandel dan is het wel prettig te weten dat een hacker er niet met je credit-card gegevens
vandoor kan gaan. Als er geheimen in een emailtje staan is het verstandig het bericht te versleutelen zodat anderen het niet kunnen
lezen.
Al eeuwen lang probeert men door geheimschrift informatie af te schermen voor nieuwsgierige ogen, maar tegenwoordig is dat nog
veel belangrijker dan vroeger.
Daardoor heeft de geheimschriftkunde of cryptografie
de laatste jaren een hoge vlucht genomen.
 17.2 Firewall, virusscanner
17.2 Firewall, virusscanner
Firewall
Een firewall is software die aanvallen van hackers buiten de deur houdt.
Een firewall werpt als het ware een ondoordringbare muur rond de computer op.
De firewall houdt op de achtergrond de veiligheid van de computer in de gaten en blokkeert aanvallen van buitenaf.
Een firewall kan ook een heel netwerk beveiligen. Zo'n firewall is er niet alleen als software, maar ook als een apparaat dat
tussen het netwerk en het internet zit.
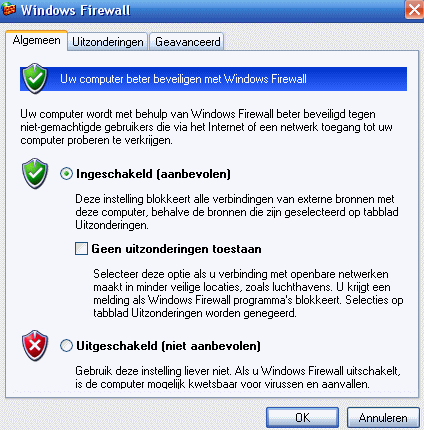
Windows XP en zijn opvolgers hebben een ingebouwde personal firewall.
Die kun je instellen door te klikken op Start → Configuratiescherm
→ Beveiligingscentrum → Windows Firewall.
Je krijgt dan onderstaand venster in beeld.
Voor oudere besturingssystemen kun je een firewall downloaden, ZoneAlarm is een bekende.
De gebruiker kan zelf regels instellen en bepaalde communicatie tussen computer en het internet toestaan
en andere afwijzen.
Een firewall zorgt ervoor dat verzoeken vanuit een netwerk of internet om bepaalde programma's op jouw computer te openen, geblokkeerd
worden, en een firewall houdt bepaalde poorten van de computer open of juist gesloten.
Een computer bevat een groot aantal poorten, alle met een nummer. Dat zijn onzichtbare onderdelen van het systeem;
iedere toepassing heeft zijn eigen poortnummer. Zo gaan bijvoorbeeld alle binnenkomende internetpagina's door poortnummer 80,
als je email verstuurt gaat het door poortnummer 25 en als het binnenkomt gaat het meestal via poortnummer 110.
De firewall kan bepaalde poorten sluiten en open stellen, voor inkomend of uitgaand verkeer, of beide.
Virussen, spyware, trojaans paard
Denk er om: een firewall is geen virusscanner. Een virusscanner moet je meestal zelf installeren.
Een virus is een programmaonderdeel, dat zich aan bepaalde programma's
kan hechten en er na verloop van tijd voor zorgt dat
de computer niet goed meer werkt.
Een virus kan alleen worden verspreid door het uitvoeren van een geïnfecteerd programma (dat vaak als bijlage bij een
emailtje wordt verstuurd), dus door menselijk handelen.
Een virus kan ook via een macro worden verspreid, of via javascript op een site,
of via ActiveX.
(ActiveX-besturingselementen zijn kleine programma's, ook wel invoegtoepassingen genoemd, die worden gebruikt op internet.
Ze zijn soms nodig om bepaalde dingen te kunnen laten zien, of soms worden ze gebruikt bij het installeren van bepaalde updates)
Bekende virusscanners zijn die van Norman, McAfee, of
Kaspersky. Ook AVG en
Avast zijn bekend, en die kun je gratis downloaden.
Virusscanners maken gebruik van verschillende technieken om te controleren op virussen:
-
De fingerprinttechniek
Virusscanners maken gebruik van virusdefinities, waarin voor elk bekend virus de fingerprint (= vingerafdruk) wordt vastgelegd.
De fingerprint van een virus is een stukje code van het virus dat altijd hetzelfde is.
Aan de hand van de fingerprint kan een scanner een virus dan herkennen.
Op deze manier kunnen alleen virussen worden ontdekt waarvan de fingerprint bekend is.
Daarom is het belangrijk de virusscanner vaak te updaten.
-
De checksumtechniek
Bij de checksumtechniek wordt gebruik gemaakt van de checksums van alle bestanden op de computer.
Een checksum van een bestand is een controlegetal dat de lengte van het bestand bevat.
Als een programma wordt besmet wordt het bestand langer en dan klopt het controlegetal niet meer.
De virusscanner controleert dus steeds of de checksum van elk bestand nog hetzelfde is als de checksum die is vastgelegd
in een lijst.
-
De heuristische techniek
Een heuristische scanner controleert bestanden op eigenschappen die typisch zijn voor virussen.
Dan heb je ook nog spyware.
Bij bepaalde soorten gratis software, die je kunt downloaden, kan het voorkomen dat er een ongewenst
programma meegeïnstalleerd
wordt. Deze programma's verzamelen meestal informatie over je surfgedrag en/of tonen advertenties in je browserscherm. Of in
het ergste geval verzamelt het programma bankgegevens, wachtwoorden en creditcardnummers van de computergebruiker.
Dat soort ongewenste programma's wordt spyware genoemd. Je hebt speciale anti-spyware programma's. Soms zit
het in een virusscanner ingebakken.
Spyware installeert zich vaak via webpagina's door gebruik te maken van de fouten die zich in Internet Explorer bevinden.
Een voorbeeld hiervan is de overname van je startpagina, dat wordt browser hijack genoemd.
Als je Firefox gebruikt heb je hier minder last van, en Firefox beschermt je ook meer tegen onder andere adware.
Adware laat reclame boodschappen aan de gebruiker zien.
Malware is de verzamelnaam voor ongewenste software dat zich installeert op je pc.
Een worm.
Een worm is vergelijkbaar met een virus, maar een worm kan worden verspreid van computer naar computer zonder menselijk handelen.
Het grootste gevaar van een worm is zijn vermogen om zichzelf te repliceren. Het kan bijvoorbeeld een kopie van zichzelf sturen naar
iedereen in je email-adressenboek.
Een worm kan je pc ook omvormen tot een zogenaamde zombie of bot;
je computer wordt dan onderdeel van een groot netwerk (het zogenaamde
botnet) en het kan dan
bijvoorbeeld gebeuren dat jouw computer spammail gaat versturen zonder dat je het in de gaten hebt.
Doordat wormen zich zelfstandig verspreiden gaat dit veel sneller dan bij virussen. In de animatie hieronder
is te zien hoe de worm Witty zich in 2004 binnen 2 uur over de hele wereld verspreidde.
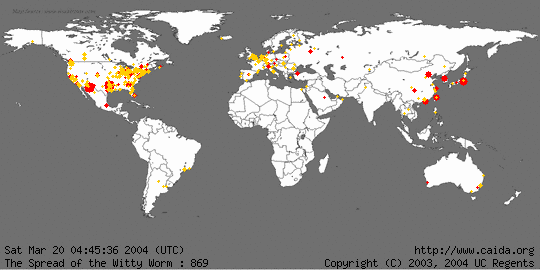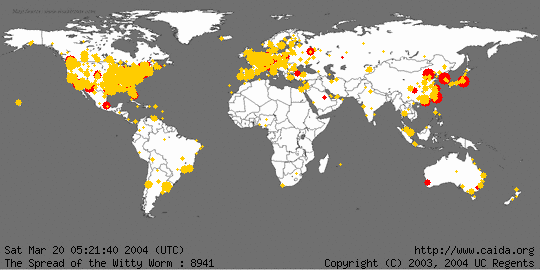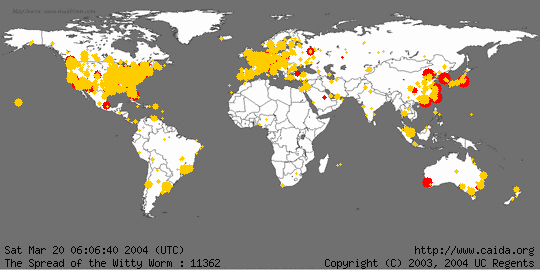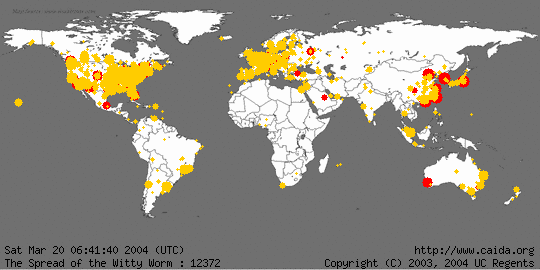
Een Trojaans paard.
 Een trojaans paard is een speciaal soort spyware. Het is een klein programma dat zich, vaak
vermomd als een nuttig programma, op je harde schijf nestelt.
Er wordt op een site gedaan alsof je een handig hulpprogramma, een leuke screensaver, of een gratis
fotobewerkingsprogramma kunt downloaden. Je downloadt het bestand en besmet zo je eigen computer.
En dat programma maakt je pc vervolgens stiekem toegankelijk voor andere
gebruikers.
Het programma kan bijvoorbeeld ook wachtwoorden stelen, bestanden verwijderen, enz.
Een trojaans paard is een speciaal soort spyware. Het is een klein programma dat zich, vaak
vermomd als een nuttig programma, op je harde schijf nestelt.
Er wordt op een site gedaan alsof je een handig hulpprogramma, een leuke screensaver, of een gratis
fotobewerkingsprogramma kunt downloaden. Je downloadt het bestand en besmet zo je eigen computer.
En dat programma maakt je pc vervolgens stiekem toegankelijk voor andere
gebruikers.
Het programma kan bijvoorbeeld ook wachtwoorden stelen, bestanden verwijderen, enz.
Een trojaans paard wordt ook wel een backdoor genoemd.
Phishing.
Phishing is een vorm van oplichterij, waarbij geprobeerd wordt achter allerlei persoonlijke
informatie te komen, zoals creditcardnummers, wachtwoorden, enz.
Een phisher doet zich meestal voor als een bekende organisatie, bijvoorbeeld een bank.
De phisher verstuurt miljoenen emails naar willekeurige mensen, en daarin verzoekt de phisher op een link te klikken zodat de
gegevens gecontroleerd kunnen worden.
Je klikt door op een link, en je komt op een vervalste website.
De valse website ziet er meestal net zo uit als de website van je bank en gebruikt soms delen van de echte website.
Je moet dan zogenaamd inloggen met je inlognaam en wachtwoord en/of creditcard-nummer, en zo krijgt de fraudeur de
beschikking over jouw gegevens.
Bij phishing wordt vaak gebruik gemaakt van URL-spoofing; dat is het nabootsen van de URL van een site (er is
bijvoorbeeld één letter verschil met de echte URL), zodat je denkt de echte site te bezoeken.
Spam.
Ongevraagde berichten via e-mail wordt spam genoemd.
Hoe komen spammers nu aan deze e-mailadressen? Daarvoor worden vaak spiders gebruikt.
Een spider is een programma dat het internet afzoekt naar @-symbolen. De spider slaat het woord voor en na het
apenstaartje op in een bestand en zo worden er een hoop emailadressen gevonden.
Spam komt ook wel in de vorm van een hoax.
Een hoax is een nepwaarschuwing. De lezer van de email met de nepwaarschuwing wordt gevraagd het emailtje naar zoveel mogelijk
mensen door te sturen.
Om spamberichten via formulieren op internet tegen te gaan wordt wel gebruik gemaakt van een captcha.
Formulieren op internet worden soms automatisch ingevuld met reclameteksten, en om te voorkomen dat dat gebeurt kan er
gebruik worden gemaakt van een captcha.
(Captcha is een afkorting voor "Completely Automated Public Turingtest to tell Computers and Humans Apart")
Een voorbeeld van een captcha zie je hieronder. Het is de bedoeling dat je de tekst overtypt, en alleen als de tekst goed is
overgenomen op het formulier wordt het verder verwerkt. Een bot kan zo'n moeilijk te lezen tekst niet automatisch invoeren.
|