| |
De rij van Fibonacci en de Gulden Snede
 |
Fibonacci (zoon van Bonaccio) was een Italiaans koopman. Hij heette eigenlijk Leonardo da Pisa en leefde van 1175 - 1250. Hij had veel belangstelling voor wiskunde en schreef verschillende boeken over rekenkunde en algebra. Zo publiceerde hij in 1202 het boek Liber Abaci. Een van de problemen uit dit boek ga je straks bestuderen. Het gaat over een groeiende konijnenfamilie.
In de 19e-eeuw schreef de franse wiskundige Edouard Lucas een vierdelig boek vol met recreatieve wiskunde en hij heeft aan de oplossing van het konijnenprobleem uit Liber Abaci de naam Fibonacci verbonden. Vandaar dat de speciale rij getallen die bij dit probleem hoort nog steeds de rij van Fibonacci heet.
De verhouding van twee opeenvolgende getallen van de rij van Fibonacci gaat op den duur naar de zogenaamde Gulden Snede. Dat blijkt een bijzondere verhouding te zijn, die op veel plaatsen in de natuur voorkomt, en hij wordt ook
wel de Divina Proportia (de Goddelijke Verhouding) genoemd.
|
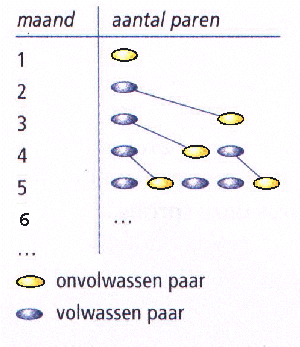
- Neem aan dat een konijnenpaar eens per maand één paar jongen krijgt, een mannetje en een vrouwtje.
Dit nieuwe paar heeft een maand nodig om volwassen en geslachtsrijp te worden en een maand later komen hun eerste jongen ter wereld. Ze krijgen vervolgens eens per maand ook weer één paar jongen, een mannetje en een vrouwtje.
Ga er vanuit dat de omstandigheden ideaal zijn. Dat wil zeggen dat er geen konijnen sterven en dat de populatie op deze manier ongehinderd blijft doorgroeien. Je begint met één onvolwassen paar en je wilt weten hoeveel konijnenparen er bij het begin van elke volgende maand zullen zijn. In het schema hiernaast zie je hoe dat de eerste maanden verloopt.
- Neem het schema over en breid het uit voor de maanden 6, 7 en 8.
- Het nummer van de maand in opdracht 1 kun je aangeven met n en de aantallen konijnenparen aan het begin van
elke maand met F(n). Dan is dus F(1) = 1, F(2) = 1, F(3) = 2, enz.
Hieronder zie je het begin van een tabel met functiewaarden.
|
nummer van de maand n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| aantal konijnenparen F(n) |
1 |
1 |
2 |
3 |
5 |
|
|
|
- Neem de tabel over en vul hem verder in.
- Hoe kun je F(5) berekenen uit F(4) en F(3) ?
- Hoe kun je F(6) berekenen uit F(5) en F(4) ?
- Breid de tabel uit tot en met F(16).
De rij getallen 1, 1, 2, 3, 5, 8, .... waarbij elk getal (behalve de eerste twee) ontstaat als de som van
de twee voorgaande getallen heet de rij van Fibonacci.
- Het getal in de rij dat voorafgaat aan F(n) kun je aangeven met F(n-1) en het getal dat daaraan voorafgaat
met F(n-2). Voor de getallen van de rij van Fibonacci geldt dus de volgende formule :
F(n) = F(n-1) + F(n-2)
- Je kunt de getallen van de rij van Fibonacci handig met Excel bepalen.
(hoe je met Excel kunt werken kun je nalezen op de informatica-site van het LC, daar staat trouwens ook deze PO op.)
Zet in kolom A in de cellen A1 t/m A100 de getallen 1 t/m 100 (gebruik de vulgreep !).
Vul in kolom B in de cellen B1 en B2 de bovenste twee getallen in.
Welke formule moet je in cel B3 zetten om er voor te zorgen dat het juiste getal wordt berekend ?
- Kopiëer die formule naar beneden m.b.v. de vulgreep, zodat de aantallen van de rij van Fibonacci tot en met maand 100 verschijnen. Zorg er voor dat de kolom breed genoeg is.
Vul in de tabel hieronder de aantallen van de maanden ........... t/m ................ in.
|
nummer van de maand n |
|
|
|
|
|
|
|
aantal konijnenparen F(n) |
|
|
|
|
|
|
- Hoeveel dagen duurt het voordat het aantal konijnenparen boven de .............. miljoen/miljard zit ?
- Je kunt in het Excel-werkblad van opgave 2 de groeifactor per maand (dus F(n) / F(n-1) ) ook handig laten berekenen.
Die groeifactoren zetten we in kolom C
- Welke formule moet je in cel C2 zetten om er voor te zorgen dat de groeifactor van de tweede maand wordt berekend
(dat is dus het aantal in de tweede maand gedeeld door het aantal in de eerste maand)
- Kopiëer die formule naar beneden m.b.v. de vulgreep, zodat de groeifactoren tot en met maand 100 verschijnen.
Vul de groeifactoren van maand 2 t/m maand 15 in, in drie decimalen nauwkeurig.
- Die groeifactor is op den duur steeds (afgerond op 3 decimalen) 1,618
Dat klopt vanaf maand nummer 10, en aan het begin van die maand zijn er 55 konijnenparen. Kennelijk gedraagt de functie F zich vanaf die maand als een exponentiële functie. Geef de formule van die exponentiële functie : F(n) = 55 * .........
- Je kunt de aantallen die je met die exponentiële functie krijgt ook weer handig met Excel bepalen.
Zet eerst in cel D10 het getal 55 (dus hetzelfde aantal als in C10)
Welke formule moet je in cel D11 zetten om er voor te zorgen dat het juiste getal voor maand nummer 11 wordt berekend ?
- Kopiëer die formule naar beneden m.b.v. de vulgreep, zodat de aantallen tot en met maand nummer 100 verschijnen. Zorg er voor dat de kolom breed genoeg is.
Vul in de tabel hieronder de aantallen van de maanden uit vraag 3b in.
|
nummer van de maand n |
|
|
|
|
|
|
|
aantal m.b.v. exponentiële f. |
|
|
|
|
|
|
- Het getal 1,618 komt ook in een ander verband vaak voor.

- Meet van het raam hiernaast zo nauwkeurig mogelijk de lengte en de breedte in mm.
De lengte is .... mm en de breedte is .... mm.
- Deel nu de lengte door de breedte, wat is de uitkomst ?
Kunstenaars gebruiken vaak rechthoeken waarbij de verhouding van de kortste en de langste zijde ongeveer gelijk is aan 1 : 1,618. Die verhouding heet de gulden snede. En zo'n rechthoek heet een gouden rechthoek.
- Gouden rechthoeken hebben een bijzondere eigenschap.
- Teken een rechthoek met zijden van 10 cm en 16,2 cm en knip die rechthoek uit. Leg uit waarom dit (bijna) een gouden rechthoek is.
- Knip van deze rechthoek een vierkant af van 10 cm bij 10 cm. Hoe lang zijn de zijden van de rechthoek die je overhoudt ? Leg uit dat die overgebleven rechthoek ook (bijna) een gouden rechthoek is.
- Knip van de laatste rechthoek weer een vierkant. Hoe lang zijn de zijden van de rechthoek die je dan overhoudt ? Is dat ook weer een gouden rechthoek ? Leg uit !
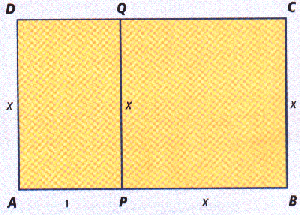
- In deze opdracht ga je berekenen wat in een gouden rechthoek de exacte verhouding is.
Om die verhouding te vinden gebruik je de figuur hiernaast.
- Als je van de gouden rechthoek ABCD een vierkant PBCQ afsnijdt, blijft er een rechthoek APQD over en dat is ook weer een gouden rechthoek.
Van die laatste rechthoek is AP = 1 en AD = x , dus de gezochte verhouding is 1 : x
In de grote rechthoek is de lengte 1 + x en de breedte is x , dus de verhouding van de kortste tot de langste is x : 1+x
Omdat ook dat een gouden rechthoek is moet die verhouding gelijk zijn als bij de kleine, dus 1 : x
In een verhoudingstabel kun je het als volgt invullen :
| kortste |
AP = 1 |
PQ = x |
| langste |
AD = x |
AB = 1 + x |
In die verhoudingstabel zijn de kruisproducten gelijk. Door die kruisprodukten te berekenen en gelijk te stellen krijg je een kwadratische vergelijking. Laat dat zien.
- Los de kwadratische vergelijking op met de abc-formule. Eén van de oplossingen is x=1,618 (in 3 decimalen) Geef die oplossing in 5 decimalen. Waarom valt het tweede oplossing af ?
Je kunt zeggen dat een lijnstuk in twee stukken is verdeeld die zich verhouden als de gulden snede als het volgende geldt:
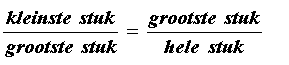
En dat geldt dan ook als de definitie van de gulden snede.
(Kijk maar in de figuur bij opgave 7. Daar geldt 1 : x = 1 : (1+x), dus AP : PB = PB : AB, dus voor de stukken op lijnstuk AB geldt:
kleinste stuk : grootste stuk = grootste stuk : hele stuk)
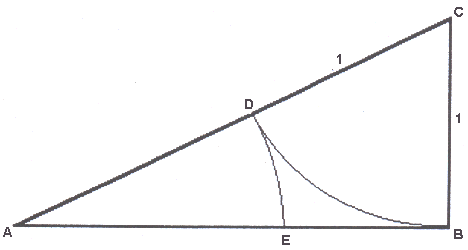
- Je kunt een lijnstuk met behulp van een passer en een driehoek gemakkelijk in twee stukken verdelen die zich verhouden volgens de Gulden Snede (zonder te meten). Dat kan op de volgende manier:
- Als dat lijnstuk AB is, dan teken je bij B een hoek van 90 graden. En dan teken je BC zo dat de lengte van BC de helft is van AB.
- Vervolgens teken je punt D op AC zo dat DC even lang is als BC (dat kan handig met een passer, zet de passerpunt in C, zet de potloodpunt op B, en teken een cirkelboog, zie de figuur)
- Daarna teken je punt E op AB zo dat AE even lang is als AD (dat kan weer handig met een passer, zet de passerpunt in A, zet de potloodpunt op D, en teken een cirkelboog, zie de figuur)
- Dan is AB in punt E verdeeld volgens de gulden snede.
Bewijs dat.
Aanwijzing: Je moet dan bewijzen dat:
kleiste stuk : grootste stuk = grootste stuk : hele stuk, anders gezegd EB : AE = AE : AB
of als breuken geschreven:
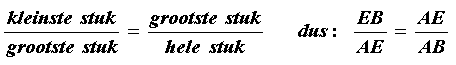
Neem aan dat BC de lengte 1 heeft. Dan heeft AB de lengte 2. De lengte van AC kun je dan berekenen.
En dan kom je er waarschijnlijk wel uit. (Denk er om dat je bij een bewijs niet mag benaderen. Gebruik de rekenmachine dus niet bij dit bewijs !)
- We gaan nu uitzoeken wat het verband is tussen de gouden rechthoek en de rij van Fibonacci.
Als je een gouden rechthoek hebt en je knipt er een vierkant af, dan is de overgebleven rechthoek weer een gouden rechthoek.
Je kunt ook het omgekeerde doen. Als je een gouden rechthoek hebt en je plakt er een vierkant aan vast dan is de nieuwe natuurlijk ook weer een gouden rechthoek.
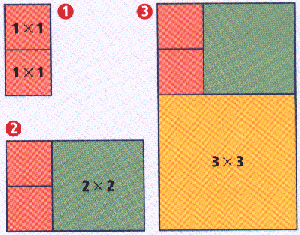
- Teken een vierkant van 1 cm bij 1 cm en leg daar nog zo'n vierkant tegenaan. Dan heb je een rechthoek van 1 cm bij 2 cm, en dat is geen gouden rechthoek maar je kunt er wel iets mee doen zodat je wel een gouden rechthoek krijgt.
- Teken er een vierkant van 2 cm bij 2 cm tegenaan.
- Breid de figuur van opdracht b uit met een rechthoek van 3 cm bij 3 cm.
- Ga verder met een vierkant van 5 cm bij cm en daarna een vierkant van 8 cm bij 8 cm.
- Geef de afmetingen van de volgende twee rechthoeken in deze rij. Maak een tekening tot en met die laatste rechthoek. Wat is in die laatste rechthoek de verhouding tussen lengte en breedte ? Is het een gouden rechthoek ?
- Welk verband is er tussen deze rechthoeken en de rij van Fibonacci ?
- Maak een tabel van de verhouding van de kortste zijde en de langste zijde en laat zien dat zo op den duur een
gouden rechthoek ontstaat.
| rechthoek |
verhouding |
| 1 cm bij 2 cm |
1 : 2 |
| 2 cm bij 3 cm |
2 : 3 = 1 : 1,5 |
| 3 cm bij 5 cm |
3 : 5 = 1 : 1,67 |
| ...... |
...... |
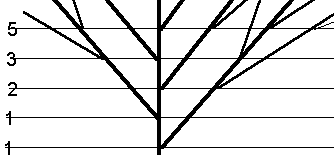
- Fibonacci-getallen kom je nogal eens in de natuur tegen.
Bij veel planten komt een zijtak uit de oksel van een blad. Deze zijtakken krijgen op dezelfde manier op hun beurt ook weer zijtakken.
Opvallend is dat een zijtak niet tegelijk met de hoofdtak een zijtak krijgt, maar de eerste 'overslaat'. In de tekening hiernaast zie je dat het aantal punten (op een bepaalde hoogte) waar een zijtak ontspringt een Fibonacci-rij vormt.
- Neem de tekening over en breid hem uit, teken hem nog drie niveau's hoger.
- Kun je een reden voor deze groeiwijze bedenken ?
-
Bijen hebben een ongewone familieboom en dat komt omdat niet alle bijen twee ouders hebben!
In een bijenkolonie is er één bijzondere vrouw: de koningin. Dan zijn er heel veel werksters, die net
als de koningin vrouwelijk zijn, maar in tegenstelling tot haar geen eitjes leggen. Tenslotte zijn er
nog de darren. Dit zijn mannelijke bijen die ontstaan uit onbevruchte eitjes van de koningin. Een
dar heeft een moeder, maar geen vader! Alle vrouwelijke bijen komen uit bevruchte eitjes en hebben
dus twee ouders. De meeste vrouwtjes worden werkster. Enkele uitverkorenen echter krijgen
speciale voeding en worden koningin. Zij zullen later zelf een nieuwe kolonie starten.
Hoe ziet de stamboom van een dar er uit? (V=vrouwtje, M=mannetje)
- Het begint met een dar: M
- Een dar heeft 1 ouder: V
- Een dar heeft twee grootouders: M en V
- Een dar heeft drie overgrootouders: V, M en V
Opdracht :-
Breid de stamboom uit, zodat er 7 generaties in beeld komen. Waar zie je de rij van Fibonacci?
- Als je de rijen van je stamboom als volgt herschrijft: V=1 en M=0, dan krijg je de volgende
rij: 0, 1, 01, 101, …….. Vul dat eens aan.
- De rij binaire getallen die je zo krijgt heet De gouden ketting van Fibonacci. Er zit een
bijzondere regelmaat in de ketting. Wat is de relatie tussen deze rij en de twee voorgaande
rijen?
- De gulden snede kom je ook bij hoeken tegen in de natuur.
Bladeren zijn vaak spiraalsgewijs om een stengel gerangschikt. Bij meting blijkt dat de hoek tussen twee opeenvolgende bladeren gemiddeld 137,5 º is. Die hoek wordt wel de Gulden Hoek genoemd.
In een bovenaanzicht, waarbij de bladeren als lijntjes zijn voorgesleld, ziet het er als volgt uit:
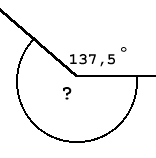
- Welke verhouding hebben die hoek en de hoek die er naast zit (waar het vraagteken in staat) ?
- En welke verhouding hebben de hoek met het vraagteken en 360 º ?
- Onderzoeksopdracht.
Het is de bedoeling dat je nog één van de volgende vier opdrachten en of onderzoeken doet.
Voor jouw groepje is dat opdracht .....
-
In een regelmatige vijfhoek komt de gulden snede ook voor. De stukken waarin de diagonalen elkaar verdelen verhouden zich als de gulden snede.
Hieronder zie je links een vijfhoek met de diagonalen, rechts dezelfde vijfhoek met drie van vijf diagonalen.
 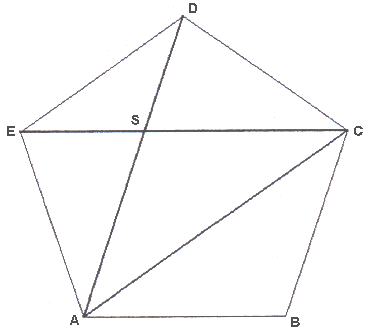
- Meet de stukken van de diagonaal (ES en SC) en controleer of ze zich ongeveer verhouden als 1 : 1,618
- Je kunt zonder te meten bewijzen dat het inderdaad de Gulden Snede is. Bekijk daarvoor de rechter vijfhoek.
Je weet de volgende dingen:
-
Uit symmetrie-overwegingen kun je zeggen dat EC evenwijdig is aan AB.
- Om dezelfde reden is AD evenwijdig aan BC.
- Dan is ABCS is een parallellogram, en dus is AB even lang als CS, dus de zijde van de vijfhoek is even lang
als het langste stuk van de diagonaal.
- De zijden van de vijfhoek zijn allemaal even lang, en de diagonalen van de vijfhoek zijn ook allemaal even lang.
- Omdat EC evenwijdig is aan AB is driehoek ACS gelijkvormig met driehoek DES.
Bewijs nu dat:
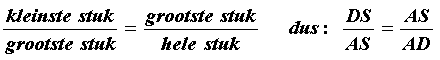
- Tel het aantal blaadjes van de buitenste bloempjes bij een aantal composieten, bijv. bij de margriet, het duizendblad, de aster, enz. Welke getallen kom je tegen bij welke bloemen en heeft dat iets met de Fibonacci-rij
te maken ?
(als je niet aan zulke bloemen kunt komen kun je het zelf niet tellen, maar zoek dan op internet uit hoe het zit met die aantallen)
- De Fibonacci-getallen geven we vaak aan met F1 , F2 , F3 , F4 , enz.
Er geldt dus F1=1, F2=1 , F3=2 , F4=3 , enz.
Voor Fibonacci-getallen geldt voor alle waarden van n=1, 2, 3, ... : F1 + F2 + F3 + .... + Fn = Fn+2 - 1
Bewijs dit d.m.v. volledige inductie (zie onderaan): laat eerst zien dat het klopt voor n=4, n=5, n=6 en n=7
Toon daarna het "domino-effect" aan.
-
In een gelijkbenige driehoek met hoeken van 72, 72, en 36 graden komt de gulden snede ook voor. De zijden verhouden zich als de gulden snede.
Hieronder zie je links zo'n driehoek, rechts dezelfde driehoek met de bissectrice (= deellijn) van hoek A
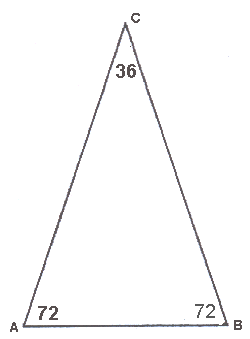 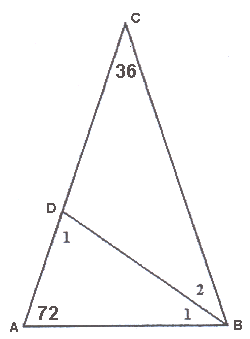
- Meet de zijden van de linker driehoek (AB en AC) en controleer of de verhouding ongeveer 1 : 1,618 is.
- Je kunt zonder te meten bewijzen dat het inderdaad de Gulden Snede is. Bekijk daarvoor de rechter driehoek.
Je weet de volgende dingen:
-
Omdat BD de deellijn van hoek B is, zijn hoek B1 en B2 beide 36 graden.
- In een driehoek zijn de drie hoeken samen 180 graden, dus hoek D1 is 72 graden.
- Dan is driehoek ABD dus gelijkbenig, en daaruit volgt dat AB even lang is als BD
- De hoeken van driehoek ABD en van ABC zijn gelijk, dus die twee driehoeken zijn gelijkvormig.
Bewijs nu dat voor de stukken, waarin zijde AC wordt verdeeld, geldt:
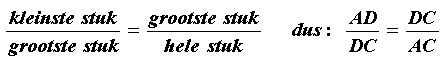
Waarom is DC even lang als AB ?
En waarom is de verhouding AB : AC dan de verhouding van de Gulden Snede ?
 Tel bij een aantal boomsoorten het aantal bladeren tot je één tegenkomt die op de zelfde lijn zit als
de eerste. Welke getallen kom je tegen bij welke bomen en heeft dat iets met de Fibonacci-rij te maken ?
Tel bij een aantal boomsoorten het aantal bladeren tot je één tegenkomt die op de zelfde lijn zit als
de eerste. Welke getallen kom je tegen bij welke bomen en heeft dat iets met de Fibonacci-rij te maken ?
(als er geen bladeren aan de bomen zitten als je deze opdracht moet doen, zoek dan op internet uit hoe het zit met die aantallen)
- De Fibonacci-getallen geven we vaak aan met F1 , F2 , F3 , F4 , enz.
Er geldt dus F1=1, F2=1 , F3=2 , F4=3 , enz.
Voor Fibonacci-getallen geldt voor alle waarden van n=1, 2, 3, ... :
F2 + F4 + F6 + .... + F2n = F2n+1 - 1
Bewijs dit d.m.v. volledige inductie (zie onderaan): laat eerst zien dat het klopt voor n=4, n=5, n=6 en n=7
Toon daarna het "domino-effect" aan.
- De Fibonaccirij is een bijzonder geval van een Lucas-rij.
Een Lucas-rij kun je vormen door met twee gehele startgetallen a en b te beginnen en elk volgende getal te vormen als de som van zijn beide voorgangers.
Dan is F(1)=a , F(2) = b, F(3)= a+b, F(4)= a+2b, F(5)= 2a+3b, enz.
- Geef de eerste 15 getallen van de Lucas-rij die begint met de getallen 2 en 4. Dat kun je handig doen met Excel (zie opdracht 3)
- De verhouding van de Gulden Snede is 1 : 1,618 of exact 1 : ½(1+ Ö5)
Als je het getal ½(1+ Ö5) voorstelt door de letter g (van goud) dan is de rij
1, g, g², g³, enz. een Lucas-rij. Toon dat aan voor de eerste drie getallen, dus bewijs dat 1 + g = g²
(Denk er om dat je bij een bewijs niet mag benaderen. Gebruik de rekenmachine dus niet bij dit bewijs !)
1, g, g²
- Als er geldt dat 1+ g = g² dan geldt er natuurlijk ook g + g² = g³ Waarom?
En natuurlijk geldt dan ook g² + g³ = g4, enz. Waarom?
Dus de rij 1, g, g², g³, enz. is een Lucas-rij.
- Meet enkele dingen in jullie huis en/of een gebouw en/of een tekening op en schrijf de dingen op met de bijbehorende maten die zich verhouden als de gulden snede.
- De Fibonacci-getallen geven we vaak aan met F1 , F2 , F3 , F4 , enz.
Er geldt dus F1=1, F2=1 , F3=2 , F4=3 , enz.
Voor Fibonacci-getallen geldt voor alle waarden van n=1, 2, 3, ... :
F1 + F3 + F5 + .... + F2n - 1 = F2n
Bewijs dit d.m.v. volledige inductie (zie onderaan): laat eerst zien dat het klopt voor n=4, n=5, n=6 en n=7
Toon daarna het "domino-effect" aan.
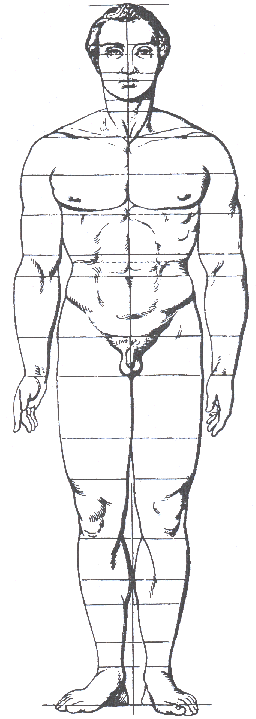
Je komt de gulden snede ook tegen in het lichaam van de mens.
- Op welke plaatsen bij de mens kom je de gulden snede tegen ? (zie de figuur rechts)
- Je weet vast wel dat een vel kopieerpapier een A4 genoemd wordt.
Bij een A4'tje heb je een andere verhouding dan de gulden snede. Als je een A4 in tweeën knipt blijft de
verhouding van lengte en breedte hetzelfde. Hoe is die verhouding dus? Leg dat uit (gebruik geen benaderingen, dus gebruik je rekenmachine niet).
Welke dingen hebben de vorm van een A1, welke die van een A2 ?
-
De Fibonacci-getallen geven we vaak aan met F1 , F2 , F3 , F4 , enz.
Er geldt dus F1=1, F2=1 , F3=2 , F4=3 , enz.
Voor Fibonacci-getallen geldt voor alle waarden van n=1, 2, 3, ... :
(F1)2 + (F2)2 + (F3)2 + .... +
(Fn)2 = Fn * Fn+1
Bewijs dit d.m.v. volledige inductie (zie onderaan): laat eerst zien dat het klopt voor n=4, n=5, n=6 en n=7
Toon daarna het "domino-effect" aan.
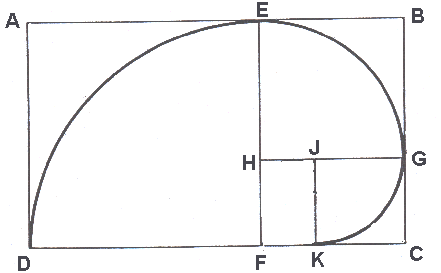
- Teken de zogenaamde Gulden Snede spiraal. Dat doe je als volgt:
Begin met een gulden rechthoek van 16 cm bij 25,9 cm.
Als je het onderste vierkant van 16 bij 16 er afhaalt, ontstaat een rechthoek van 9,9 bij 16, en dat is weer een gulden rechthoek. Als je daar het linker vierkant van 9,9 bij 9,9 afhaalt, ontstaat weer een gulden rechthoek, en zo kun je verder gaan.
Teken in het onderste vierkant een kwart cirkel, teken in het volgende vierkant weer een kwart cirkel, en ga zo steeds
verder (zie figuur). Ga zover door als je kunt. Zo krijg je een hele mooie spiraal, en dat wordt de Gulden Snede spiraal
genoemd.
Deze opdracht moet je uitvoeren in groepjes van 2.
Je maakt er een schriftelijk verslag van.
- Het verslag bevat een voorblad waarop de namen van de leden van het groepje en de titel van de opdracht.
- Dan de inhoudsopgave.
- Dan de uitwerking van de opdrachten 1 t/m 13. Je moet het zo beschrijven dat het ook te volgen is voor iemand die het opdrachtenblad niet heeft.
- Verder moet je niet alleen de antwoorden opschrijven maar je moet ook uitleggen hoe je aan het antwoord gekomen bent. .
- Je voegt aan het verslag ook een logboek toe, daarin staat beschreven wie wat en wanneer gedaan heeft.
- Het verslag lever je .................................. persoonlijk bij me in.
- De beoordeling gaat via STIP :S=struktuur , T=techniek en taal, I=inhoud, P=presentatie en proces
Volledige inductie
Hoe bewijs je dat iets voor oneindig veel waarden geldt? Met volledige inductie! Dat leggen we uit aan de hand
van twee voorbeelden, die niets met Fibonacci-getallen hebben te maken.
Zelf moet je het toepassen op Fibonacci-getallen (zie je opdracht bij 12)
Voorbeeld 1:
We willen bewijzen dat voor alle positieve gehele waarden van n (dus n = 1,2,3,...) geldt
dat 3 2n+1 + 2 n-1 deelbaar is door 7.
Voor n=1 krijg je: 3 2n+1 + 2 n-1 = 3 3 + 2 0 = 27 + 1 = 28, en dat is deelbaar door 7
Voor n=2 krijg je: 3 2n+1 + 2 n-1 = 3 5 + 2 1 = 243 + 2 = 245, en dat is deelbaar door 7
En zo kun je doorgaan. Maar al controleer je het ook nog voor n=3 en n=4 en n=5, dan weet je nog steeds niet zeker dat
het ook voor n=6 enz. geldt.
Hoe bewijs je dan wel dat het voor iedere waarde van n geldt ? -
Volledige inductie werkt met het domino-effect.
- Voor deze methode hoef je de formule maar voor één geval te controleren, hier voor n=1.
- Verder moet je het domino-effect aantonen. Dat houdt in dat je kunt aantonen dat, als de formule voor een
bepaald getal klopt, het ook voor het volgende getal klopt.
- Als je n=1 gecontroleerd hebt, heb je de eerste steen omgegooid.
- Met het domino-effect volgt dan ook de tweede steen, de derde steen, enzovoort.
Met volledige inductie gaan we nu bewijzen dat voor alle positieve gehele waarden van n geldt:
3 2n+1 + 2 n-1 is deelbaar door 7.
Daarvoor moeten we twee dingen doen: namelijk de formule bewijzen voor n=1 en het domino-effect aantonen.
-
Voor n=1 hebben we het al aangetoond, maar we doen het nog eens.
Voor n=1 krijg je: 3 2n+1 + 2 n-1 = 3 3 + 2 0 = 27 + 1 = 28, en dat is deelbaar door 7
De eerste steen is omgevallen.
-
In de volgende stap van het bewijs moeten we aantonen dat als de formule waar is voor het getal n, de formule ook
waar is voor het volgende getal n+1.
- Stel dus dat de formule klopt voor een bepaalde waarde van n. (dat noem je wel de inductieveronderstelling):
(Let op: we gaan er vanuit dat de formule voor slechts één bepaalde waarde van n geldt en niet voor alle n).
- We gaan er dus vanuit dat 3 2n+1 + 2 n-1 deelbaar is door 7
De vraag is nu of we aan kunnen tonen dat 3 2(n+1)+1 + 2 (n+1)-1 dan ook deelbaar is door 7
Dat kunnen we inderdaad aantonen.
- Want: 3 2(n+1)+1 + 2 (n+1)-1 = 3 2n+3 + 2 n
- Dat is gelijk aan 3 2.3 2n+1 + 2 1 .2 n-1
(tel de exponenten maar op: 2 + 2n+1 = 2n + 3 en 1 + n-1 = n, dus het klopt)
- Dat is gelijk aan 9.3 2n+1 + 2.2 n-1
- Daarvan kun je maken 7.3 2n+1 + 2.3 2n+1 + 2.2 n-1
(want 7.3 2n+1 + 2.3 2n+1 = 9.3 2n+1 )
- En dat is gelijk aan 7.3 2n+1 + 2.(3 2n+1 + 2 n-1) ( 2 buiten haakjes halen)
Nu kun je laten zien dat het deelbaar is door 7.
- Natuurlijk is 7.3 2n+1 deelbaar door 7, want als je iets keer 7 doet is het resultaat deelbaar door 7
- Verder gingen we er vanuit dat 3 2n+1 + 2 n-1 deelbaar is door 7, dan is ook
2.(3 2n+1 + 2 n-1) deelbaar door 7.
- En als je twee getallen optelt, die allebei deelbaar zijn door 7, dan is het resultaat ook deelbaar door 7.
- Dus 7.3 2n+1 + 2.(3 2n+1 + 2 n-1) is deelbaar door 7.
- Omdat de formule waar is voor n=1 en de inductiestap ook bewezen is, geldt de bewering voor alle n volgens het domino-effect.
Voorbeeld 2:
We willen bewijzen dat voor alle positieve gehele waarden van n (dus n = 1,2,3,...) geldt
dat 1 3 + 2 3 + 3 3 + 4 3 + ....... + n 3 = 0.25 n 2 (n+1) 2
-
Voor n=1 krijg je: 1 3 = 0.25 x 1 2 x (1+1) 2 , en dat klopt
Voor n=2 krijg je: 1 3 + 2 3 = 0.25 x 2 2 x (2+1) 2 , dus 1 + 8 = 0.25 x 4 x 9 en dat klopt ook
Zo, nu hebben we het voor n=1 en voor n=2 gecontroleerd, de eerste stenen zijn omgegooid.
- Nu gaan we het domino-effect aantonen.
We moeten dus aantonen dat als de formule waar is voor het getal n, de formule ook
waar is voor het volgende getal n+1.
Stel dus dat de formule klopt voor een bepaalde waarde van n. (dat is de inductieveronderstelling):
- We gaan er dus vanuit dat 1 3 + 2 3 + 3 3 + 4 3 + ....... + n 3 = 0.25 n 2 (n+1) 2
De vraag is nu of we aan kunnen tonen dat 1 3 + 2 3 + 3 3 + 4 3 + ....... + n 3 + (n+1) 3 = 0.25 (n+1) 2 (n+2) 2
Dat kunnen we inderdaad aantonen.
- Want: 1 3 + 2 3 + 3 3 + 4 3 + ....... + n 3 + (n+1) 3 =
- = 0.25 n 2 (n+1) 2 + (n+1) 3 = (haal nu (n+1) 2 buiten haakjes)
- = (n+1) 2 (0.25 n 2 + n + 1) = (haal nu 0.25 buiten haakjes)
- = (n+1) 2 x 0.25 x (n 2 + 4n + 4) = (vervang nu (n 2 + 4n + 4) door (n + 2) 2 )
- = (n+1) 2 x 0.25 x (n + 2) 2 = (verander nu de volgorde, zet 0.25 vooraan)
- = 0.25 (n+1) 2 (n + 2) 2
Daarmee is het domino-effect aangetoond.
- En dus klopt de formule voor alle positieve gehele waarden van n
|
| |





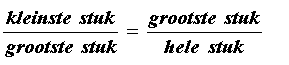

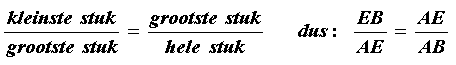




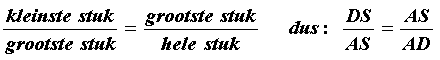


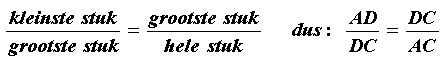
 Tel bij een aantal boomsoorten het aantal bladeren tot je één tegenkomt die op de zelfde lijn zit als
de eerste. Welke getallen kom je tegen bij welke bomen en heeft dat iets met de Fibonacci-rij te maken ?
Tel bij een aantal boomsoorten het aantal bladeren tot je één tegenkomt die op de zelfde lijn zit als
de eerste. Welke getallen kom je tegen bij welke bomen en heeft dat iets met de Fibonacci-rij te maken ?