| |

JavaLogo-opdrachten voor de PO
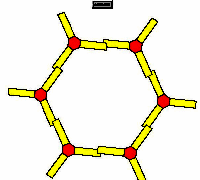
- Maak een programma voor een regelmatige zeshoek met zijden van 30 mm, rood gekleurd

- Maak een programma voor een regelmatige negenhoek met zijden van 30 mm, groen gekleurd
- Maak een programma voor een regelmatige tienhoek met zijden van 30 mm, blauw gekleurd
- Maak een programma voor een regelmatige twaalfhoek met zijden van 40 mm, geel gekleurd
- Maak een programma voor een regelmatige vijftienhoek met zijden van 40 mm, paars gekleurd
- Maak een programma voor een regelmatige twintighoek met zijden van 40 mm, grijs gekleurd
- Maak een programma voor vier rode regelmatige zeshoeken met zijden van 30 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
Zorg er verder voor dat er en invoervariabele verschijnt, waarmee je het aantal zeshoeken kunt wijzigen.

- Maak een programma voor vier groene regelmatige negenhoeken met zijden van 30 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor vier blauwe regelmatige tienhoeken met zijden van 30 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor vier gele regelmatige twaalfhoeken met zijden van 40 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor vier paarse regelmatige vijftienhoeken met zijden van 40 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor vier grijze regelmatige twintighoeken met zijden van 40 mm naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor een regelmatige negenster met zijden van 150 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier onder, dat gaat automatisch met vulAan en vulUit) rood gekleurd wordt (de hoekjes zijn 20 graden)
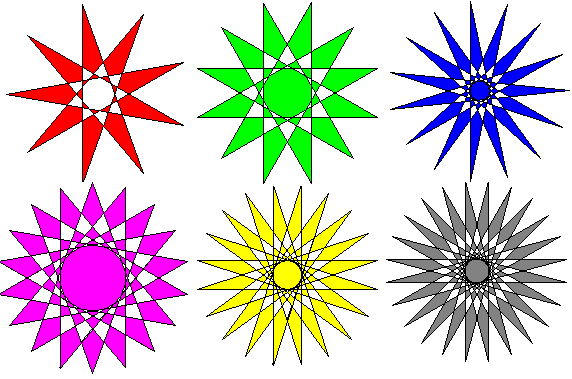
- Maak een programma voor een regelmatige twaalfster met zijden van 160 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier boven, dat gaat automatisch met vulAan en vulUit) groen gekleurd wordt (de hoekjes zijn 30 graden)
- Maak een programma voor een regelmatige vijftienster met zijden van 170 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier boven, dat gaat automatisch met vulAan en vulUit) blauw gekleurd wordt (de hoekjes zijn 12 graden)
- Maak een programma voor een regelmatige achttienster met zijden van 180 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier boven, dat gaat automatisch met vulAan en vulUit) paars gekleurd wordt (de hoekjes zijn 40 graden)
- Maak een programma voor een regelmatige twintigster met zijden van 190 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier boven, dat gaat automatisch met vulAan en vulUit) geel gekleurd wordt (de hoekjes zijn 18 graden)
- Maak een programma voor een regelmatige vierentwintigster met zijden van 200 mm, en zorg er voor dat
een gedeelte van het binnengebied (zoals hier boven, dat gaat automatisch met vulAan en vulUit) grijs gekleurd wordt (de hoekjes zijn 15 graden)
- Maak een programma voor drie van de figuren van opgave 13 (dus 3 negensterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor drie van de figuren van opgave 14 (dus 3 twaalfsterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor drie van de figuren van opgave 15 (dus 3 vijftiensterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor drie van de figuren van opgave 16 (dus 3 achttiensterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor drie van de figuren van opgave 17 (dus 3 twintigsterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
- Maak een programma voor drie van de figuren van opgave 18 (dus 3 vierentwintigsterren) naast elkaar,
met een kleine tussenruimte.
Zorg er voor dat je naam er onder verschijnt.
-
Maak een applet die de figuur hieronder tekent.
Het zijn 36-sterren, waarbij de hoekjes 10 graden zijn.
De straal van de sterren is 100 en hun kleur is blauw.
De middelpunten liggen op de hoekpunten van een (onzichtbaar) vierkant met een zijde van 200.
Zorg er voor dat je naam er onder verschijnt.

-
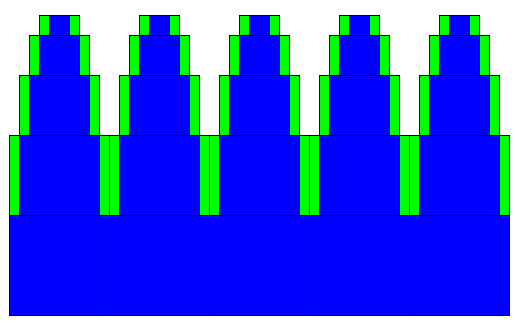
 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
Het onderste vierkant is 100 bij 100, het vierkant daar boven 80 bij 80, dan 60 bij 60, dan 40 bij 40, en het
bovenste is 20 bij 20. De vierkanten zijn blauw gekleurd. De rechthoeken zijn 10 breed, en zijn groen gekleurd.
- Maak een programma voor de volgende figuur:
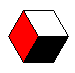 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
Hij bestaat uit drie gelijke ruiten. De zijden zijn 30. De hoeken zijn 60 en 120 graden.
De ruiten zijn rood, zwart en wit gekleurd.
Begin met de rode ruit: eerst links(30); vooruit(30); enz.
Verplaats dan de cursor naar de linker punt van de witte ruit, langs de lijntjes die er al zijn.
En geef hem de juiste richting voor het volgende ruit.
Teken dan de witte ruit, enz.
- Maak een programma voor de volgende figuur:
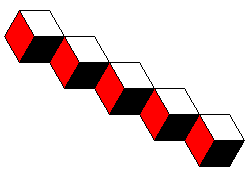
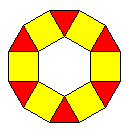 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
Hij bestaat uit driehoekjes en vierkanten. De zijden zijn 30. De hoeken van de driehoekjes zijn 60 graden.
De driehoekjes zijn rood, de vierkanten geel.
Begin met het vierkant linksmidden.
Verplaats dan de cursor naar het punt linksboven van het vierkant.
Teken dan de driehoek erboven. Verplaats dan de cursor naar het bovenste punt van de driehoek, en geef
hem de juiste richting voor het volgende vierkant.
Herhaal dat zes keer.
- Maak een programma voor de volgende figuur:
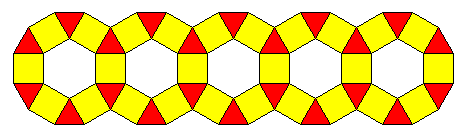
 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
Hij bestaat uit driehoekjes, de zijden van een klein driehoekje zijn 30.
De hoeken van de driehoekjes zijn 60 graden.
De driehoekjes zijn rood.
Maak eerst een procedure driehoek.
Begin dan met de driehoek linksonder. Verplaats dan de cursor naar het linker punt van het driehoekje
ernaast. En geef hem de juiste richting voor de volgende driehoek.
Herhaal dat vier keer.
Verplaats dan de cursor naar het linker punt van de driehoek in de tweede rij (boven de eerste), en geef
hem de juiste richting. Teken dan die driehoek, enz.
- Maak een programma voor de volgende figuur:
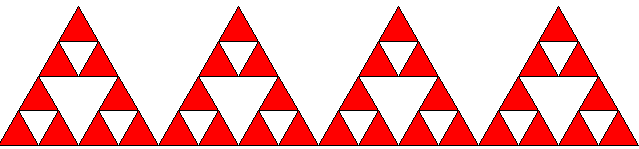
 Maak een programma voor de figuur hiernaast (links). Maak een programma voor de figuur hiernaast (links).
Hij bestaat uit drie ruiten en drie vierkanten. De zijden zijn 40. De hoeken van de ruiten zijn 30 en 150
graden.
De ruiten zijn rood, de vierkanten zijn blauw.
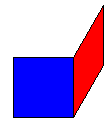 Maak eerst een procedure voor een vierkant+ruit (zie figuur rechts) Maak eerst een procedure voor een vierkant+ruit (zie figuur rechts)
Teken dan eerst het bovenste vierkant, met de ruit er rechts tegenaan. Doe dat door eerst de cursor
in de goede richting te zetten (rechts(45);), en voer dan de procedure vierkant_en_ruit uit.
Verplaats dan de cursor naar het beginpunt, en geef hem de juiste richting voor het volgende vierkant.
Voer dan de procedure vierkant_en_ruit weer uit, enz.
- Maak een programma voor de volgende figuur:
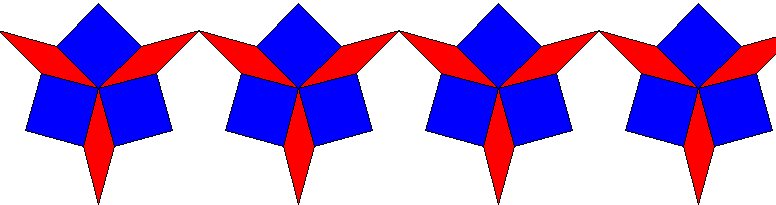
 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
De zijden zijn 30. De hoek van een punt van de ster is 30 graden, en de hoek tussen twee punten is 90 graden.
De ster is rood gekleurd.
Begin met het linker lijntje van de onderste punt, dus eerst links(15); enz.
- Maak een programma voor de volgende figuur:

-
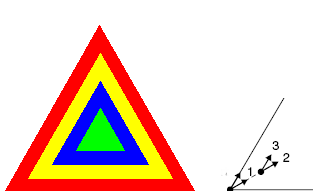
Maak een programma voor de volgende tekening :
Gebruik een methode driehoek, met twee parameters (voor de kleur en voor de grootte).
Begin met de grootste driehoek en teken de anderen daar dan overheen.
Nadat een driehoek is getekend moet de turtle naar het
startpunt van de volgende driehoek worden gebracht, in de figuur zie je rechts de bewegingen: eerst naar rechts draaien,
dan een eindje vooruit (die afstand is 46.19 mm, dat kun je m.b.v. wiskunde berekenen), dan weer naar links.
De kleuren van de driehoeken zijn rood, geel, blauw en groen (van buiten naar binnen).
De zijden van de driehoeken zijn 320, 240, 160 en 80 mm. De stap naar binnen is 46.19 mm
-
Maak een programma voor de volgende tekening :
Gebruik een methode driehoek, met twee parameters (voor de kleur en voor de grootte).
De kleinste drie hebben een zijde van 70 mm en zijn blauw, de grootste drie hebben een zijde van 210 mm en zijn groen,
en de middelste heeft een zijde van 140 mm en is rood.

-
Maak een programma voor de volgende tekening :
Gebruik een methode vierkant, met twee parameters (voor de kleur en voor de grootte).
De grote vierkanten zijn geel en hebben zijden van 140 mm, de kleine zijn groen en hebben zijden van 70 mm.
Gebruik ook een methode driehoek, met een parameter voor de kleur.
De driehoeken in het midden zijn groen en hebben rechthoekszijden van 70 mm, de anderen zijn geel en even groot.

-
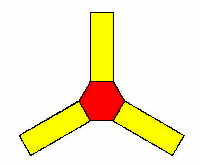
Maak een applet die de figuur hieronder tekent: hij bestaat uit een regelmatige zeshoek en drie precies aansluitende rechthoeken.
Maak de zeshoek rood en de rechthoeken geel.
De zijde van de zeshoek is (in deze opgave) 50 en een wiek is een rechthoek van 50 bij 150.
Maak gebruik van een door jou ontworpen methode 'molen(..)'.
Het handigst is dat je 'molen(.) vier parameters geeft, nl.: zijde, lengte, kleur1 en kleur2.
Zorg ook dat de cursor in deze methode weer eindigt in de beginstand.
-
Maak een applet die de figuur hieronder tekent.
De zijden van de grote ruiten zijn 120, en de hoeken zijn 30 en 150 graden.
De zijden van de kleine ruiten zijn 60, en de hoeken zijn 45 en 135 graden.

-
Maak een applet die de figuur hieronder tekent.
De hoogte van de rode huisjes is 60 en de breedte is 20, de zijden van het dak zijn 20 en de hoeken van het dak zijn 60 graden.
De hoogte van de groene huisjes is 40 en de breedte is 60, de zijden van het dak zijn 60 en de hoeken van het dak zijn 60 graden.
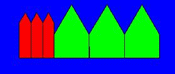
-
Maak een applet die de figuur hieronder tekent.
De hoogte van de grote rechthoeken is 200 en de breedte is 40.
De hoogte van de kleine rechthoeken is 100 en de breedte is 20.

-
Maak een applet die de figuur hieronder tekent.
De zijden van de grote rode parallellogrammen zijn 150 en 40.
Die van de grijze zijn 100 en 30.
En die van de kleine rode zijn 50 en 20.
De hoeken zijn 60 en 120 graden.
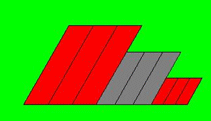
-
Maak een applet die de figuur hieronder tekent.
De hoogte van de grote rechthoeken is 200 en de breedte is 40.
De hoogte van de kleine rechthoeken is 100 en de breedte is 20.
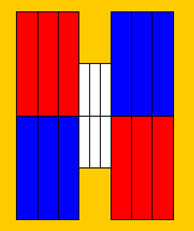
-
Maak een applet die de figuur hieronder tekent.
De zijden van de rode parallellogrammen zijn 150 en 40.
Die van de grijze zijn 100 en 30.
En die van de blauwe zijn 50 en 20.
De hoeken zijn 60 en 120 graden.
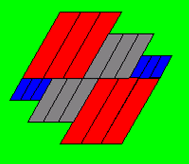

48 Maak een programma voor deze figuur.
|

49 Maak een programma voor deze figuur.
|

50 Maak een programma voor deze figuur.
|
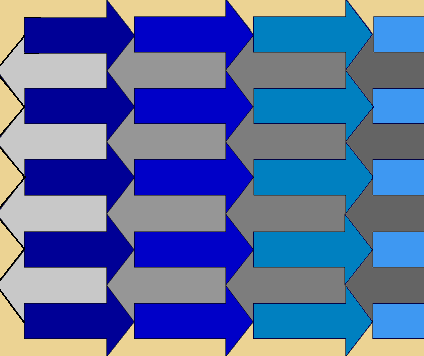
51 Maak een programma voor deze figuur.
|

52 Maak een programma voor deze figuur.
|

53 Maak een programma voor deze figuur.
|

54 Maak een programma voor deze figuur.
|

55 Maak een programma voor deze figuur.
|

56 Maak een programma voor deze figuur.
|
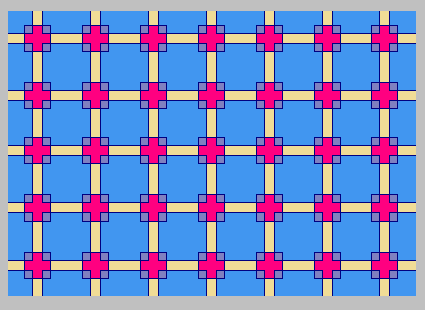
57 Maak een programma voor deze figuur.
|

58 Maak een programma voor deze figuur.
|
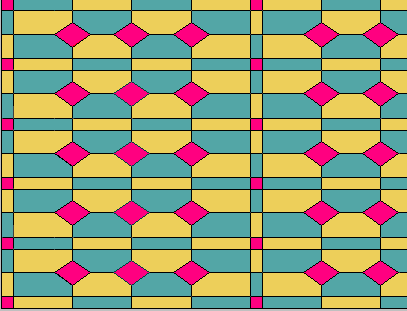
59 Maak een programma voor deze figuur.
|

60 Maak een programma voor deze figuur.
|

61 Maak een programma voor deze figuur.
|

62 Maak een programma voor deze figuur.
|

63 Maak een programma voor deze figuur.
|
-
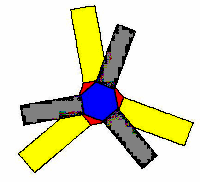
Maak een applet die de figuur hieronder tekent: hij bestaat uit een regelmatige zeshoek en drie precies aansluitende rechthoeken.
Maak de zeshoek rood en de rechthoeken geel.
De zijde van de zeshoek is (in deze opgave) 50 en een wiek is een rechthoek van 50 bij 150.
Maak gebruik van een door jou ontworpen methode 'molen(..)'.
Zorg er voor dat de molen gaat draaien na een klik op de animatie-knop.
Ook de draaisnelheid is (vooruit en achteruit) regelbaar door middel van een invoervariabele, met waarden van -4 t/m 4.
Daarbij betekent 4 dat de snelheid 4 keer zo snel als normaal is (vooruit), en bijvoorbeeld -2 betekent dat de snelheid 2 keer zo snel
als normaal is (achteruit).
Bij verandering van snelheid moet de molen doordraaien.

-
Maak een applet die twee molens tekent van de vorm als in de vorige opgave, die om dezelfde as draaien (dus hetzelfde middelpunt hebben).
De achterste molen is die van de vorige opgave, de voorste heeft een blauwe zeshoek met zijde 40 en grijze wieken met afmetingen 40
en 125.
Na een druk op de knop 'Animatie' draait de achterste molen tegen de wijzers van de klok in,
de voorste draait twee keer zo hard de andere kant op, om het middelpunt
-
Maak een applet die een draaiende molen tekent met de eigenschappen van twee opgaven hiervoor, maar waarbij de maten veranderd
kunnen worden door middel van invoervariabelen.
De kleinste lengte voor de zijde van de zeshoek is 3, de grootste is 70.
De grootste lengte van de wiek is 175.
-
Maak een applet waarin 6 draaiende molentjes (redelijk snel, tegen de wijzers van de klok in) zoals
in drie opgaven hiervoor (met maten 20, 20, 75) getekend worden met hun middelpunten op de hoekpunten van een (onzichtbare) zeshoek
met zijde 175.
Deze hele figuur draait langzaam met de wijzers van de klok mee rond het middelpunt van de grote zeshoek.
Let op dat je de draaisnelheden niet zo kiest dat het lijkt of de molentjes stil staan!
-
Maak een applet die de figuur hieronder tekent.
Het zijn 36-sterren, waarbij de hoekjes 10 graden zijn.
De straal van de sterren is 100 en hun kleur is blauw.
De middelpunten liggen op de hoekpunten van een (onzichtbaar) vierkant met een zijde van 200.

-
Maak een applet die de figuur van de vorige opgave tekent.
Maak het zo dat, na een druk op de knop 'animatie', de sterren beginnen te draaien om hun middelpunt:
die linksboven en rechtsonder tegen de wijzers van de klok in en de andere twee de andere kant op.
-
Maak een applet die de figuur van twee opgaven hiervoor tekent.
Maak het zo, dat de straal van de sterren instelbaar is met een invoervariabeleknop.
De straal moet minimaal 3 zijn en maximaal 150.
Bij verandering van de straal blijft het middelpunt van de figuur op zijn plaats.
-
Maak een applet die de figuur van drie opgaven hiervoor tekent.
Maak het zo dat, na een druk op de knop 'animatie', de sterren beginnen te draaien, allemaal
dezelfde kant op.
Maak het verder zo, dat de draaisnelheid van de sterren (vooruit en achteruit maximaal 4 graden per stapje) instelbaar is met een
invoervariabeleknop.
-
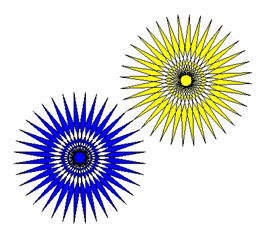
Maak een applet die de figuur hieronder tekent.
Het zijn 36-sterren met straal 100, waarbij de hoekjes 10 graden zijn.
De blauwe ster heeft zijn middelpunt in het middelpunt van het beeld, de gele ster draait om de blauwe ster heen.
Daarbij is de afstand van de middelpunten gelijk aan 200.
Maak het zo dat de gele ster ook om zijn eigen middelpunt draait.
-
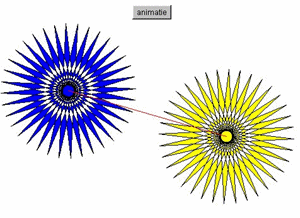
Maak een applet die de figuur hieronder tekent.
Het zijn 36-sterren met straal 100, waarbij de hoekjes 10 graden zijn.
De middens van de sterren zijn verbonden door een rode lijn.
Daarbij is de afstand van de middelpunten gelijk aan 200.
Bij klikken in (het hart van) de gele ster is die te verslepen terwijl de andere ster op zijn plaats blijft
en de twee sterren toch door middel van een rode lijn met elkaar verbonden blijven.
-
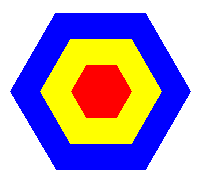
Maak een applet die de figuur hieronder tekent.
Het zijn drie regelmatige zeshoeken met hetzelfde middelpunt.
De zijde van de kleinste is 50, van de middelste 100 en van de grootste 150.
De kleuren zijn rood, geel en blauw (van binnen naar buiten).
-
Maak een applet die de figuur van de vorige opgave tekent.
Na een druk op de knop 'Animatie' gaan de zeshoeken tegen de wijzers van de klok in draaien, om hun middelpunt.
De gele zeshoek draait twee keer zo snel als de rode en de blauwe drie keer zo snel.
-
Maak een applet die de figuur van twee opgaven hiervoor tekent.
Maak het zo, dat na een muisklik binnen de gele zeshoek de hele figuur naar een willekeurige plaats op het scherm
versleept kan worden.
Bij klikken buiten de gele zeshoek kan de figuur niet verplaatst worden.
-
Maak een applet die de figuur hieronder tekent.
Het zijn regelmatige zeshoeken met hetzelfde middelpunt.
De zijde van de kleinste is 50, van de middelste 100 en van de grootste 150.
De kleuren zijn rood, geel en blauw (van binnen naar buiten).
De twee grootste zeshoeken raken elkaar met de hoekpunten.
Bij horizontaal slepen met de muis draaien beide figuren (even snel)
om hun eigen middelpunt, in tegengestelde richtingen.

-
Maak een applet die de figuur van de vorige opgave tekent.
Het zijn regelmatige zeshoeken met hetzelfde middelpunt.
De zijde van de kleinste is 50, van de middelste 100 en van de grootste 150.
De kleuren zijn rood, geel en blauw (van binnen naar buiten).
De twee zeshoeken raken elkaar met de hoekpunten.
Bij verticaal slepen worden de afmetingen van de figuren
(even veel) veranderd waarbij de afstand van de middelpunten zodanig wordt aangepast dat
de twee grootste zeshoeken elkaar met de hoekpunten blijven raken.
-
Maak een applet die de figuur hieronder tekent.
Het zijn vijf vierkanten met zijde 100.
De kleuren zijn rood (de middelste), en blauw (de rest).

-
Maak een applet die de figuur van de vorige opgave tekent.
Na een druk op de knop 'Animatie' gaan de blauwe vierkanten tegen de wijzers van de klok in draaien.
Het rode vierkant draait rechtsom, met de wijzers van de klok mee. Elk vierkant draait om het midden van het betreffende vierkant.
-
Maak een applet die de figuur van twee opgaven hiervoor tekent.
Maak het zo, dat na een muisklik binnen het middelste vierkant de hele figuur naar een willekeurige plaats op het scherm
versleept kan worden.
Bij klikken buiten het middelste vierkant kan de figuur niet verplaatst worden.
-
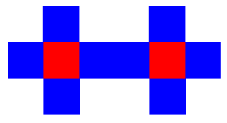
Maak een applet die de figuur hieronder tekent.
Het zijn tien vierkanten met zijde 100.
De kleuren zijn rood (de twee in het midden), en blauw (de rest).
Bij verticaal omhoog slepen met de muis draaien de beide rode vierkanten om hun middelpunt, de één linksom en
de ander rechtsom. Bij verticaal omlaag slepen draaien ze in tegengestelde richting.
-
Maak een applet die de figuur van de vorige opgave tekent.
Bij horizontaal naar rechts slepen vergroot de lengte van de zijden van alle vierkanten evenveel, bij horizontaal naar links slepen
verkleint de lengte van de zijden van de vierkanten.
De figuren mogen elkaar bij vergroten of verkleinen niet gaan overlappen, en er mag geen tussenruimte ontstaan.
-
Maak een applet, waarbij twee bloemfiguren tegen elkaar indraaien. De gele draait linksom en de rode rechtsom, twee keer zo
snel als de gele. Bij de start staan ze zoals in de linker figuur. Na een klik op Animatie gaan ze draaien, na een poosje staan ze zoals
in de rechter figuur.
 
-
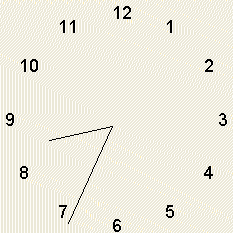
Maak een applet, waarbij een analoge klok wordt getoond. Als de grote wijzer één keer ronddraait dan verdraait de
kleine één uur. Zorg er voor dat de grote niet zo snel draait dat je het niet kunt volgen.
-
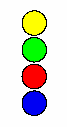
Maak een applet, waarbij je vier gekleurde cirkels onder elkaar ziet. Als je op animatie klikt gaan de cirkels om het
laagste punt (het onderste punt van de blauwe cirkel) draaien, en wel zo dat het rode twee keer zo snel gaat als het blauwe,
het groene drie keer zo snel gaat als het blauwe, en het gele in tegengestelde richting (net zo snel als de blauwe).
Verder moeten ze precies twee keer ronddraaien en dan stoppen.
Bij de start staan ze zoals in de linker figuur. Na een klik op Animatie gaan ze draaien, na een poosje staan ze zoals
in de rechter figuur.
-
Maak een programma voor het tekenen van een lessenaar (of afgekapt vierzijdig prisma):
De lengte is 100 mm, de breedte is 100 mm en de hoogte is voor 100 mm en achter 200 mm.
Zorg er voor dat alle zes vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat de tent om de z-as kan draaien (m.b.v. animatie).
Zorg er verder voor dat het bovenvlak (als er op dat vlak geklikt wordt en dan gesleept)
m.b.v. de muis gedraaid kan worden, maar niet meer dan 180 graden.
En zorg er voor dat de figuur naar links bewogen kan worden (m.b.v. een schuifinvoervariabele).

-
Maak een programma voor het tekenen van een octaeder (ook wel achtvlak genoemd, zie de figuur hier onder):
De horizontale zijden zijn 100 mm, de toppen liggen 100 mm boven en onder het grondvlak.
Zorg er voor dat alle acht vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat de piramide om de x-as kan draaien (m.b.v. een invoervariabele, die aangeeft hoeveel graden er gedraaid moet
worden).
Zorg er verder voor dat het linkerzijvlak(boven) (als er op dat zijvlak geklikt wordt en dan gesleept)
m.b.v. de muis naar beneden gedraaid kan worden.
En zorg er voor dat de figuur naar rechts bewogen kan worden (m.b.v. animatie).
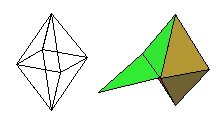
-
Maak een programma voor het tekenen van een tent (of driezijdig prisma):
De lengte is 200 mm, de breedte is 100 mm en de hoogte is 100 mm.
Zorg er voor dat alle vijf vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat de tent om een horizontale lijn door het midden van de tent kan draaien (m.b.v. animatie).
Zorg er verder voor dat het linkerzijvlak (als er op dat zijvlak geklikt wordt en dan gesleept)
m.b.v. de muis gedraaid kan worden.
En zorg er voor dat de figuur naar achteren bewogen kan worden (m.b.v. een schuifinvoervariabele).
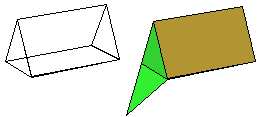
-
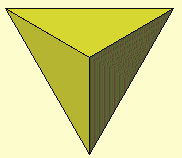
Maak een programma voor het tekenen van een viervlak:
De lengte, breedte en hoogte zijn 100 mm.
Zorg er voor dat alle vier vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat het viervlak om de z-as kan draaien (m.b.v. een invoervariabele, die aangeeft hoeveel graden er gedraaid moet
worden).
Zorg er verder voor dat het achtervlak (als er op dat zijvlak geklikt wordt en dan gesleept)
m.b.v. de muis gedraaid kan worden, maar niet meer dan 90 graden.
En zorg er voor dat de figuur naar links bewogen kan worden (m.b.v. animatie).
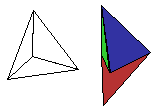
-
Maak een programma voor het tekenen van een regelmatige vierzijdige piramide:
De onderste zijden zijn 100 mm, de top ligt 150 mm boven het grondvlak.
Zorg er voor dat alle vijf vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat de piramide om de vertikale lijn door de top kan draaien (m.b.v. animatie).
Zorg er verder voor dat het voorvlak (als er op dat voorvlak geklikt wordt en dan gesleept)
m.b.v. de muis naar voren gedraaid kan worden.
En zorg er voor dat de figuur naar boven bewogen kan worden door met de muis naar boven te slepen, als er naast de figuur
geklikt is (in ieder geval niet op het voorvlak).
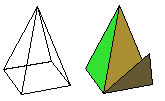
-
Maak een programma voor het tekenen van een vierzijdige piramide, waarvan het grondvlak een vierkant is, en waarvan de top
loodrecht boven het punt linksachter ligt.
De onderste zijden zijn 100 mm, de top ligt 150 mm boven het grondvlak.
Zorg er voor dat alle vijf vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
En zorg er voor dat de piramide om de vertikale lijn door de top kan draaien, en dat dat gebeurt als je naast
de kubus klikt (of in ieder geval niet op het rechter zijvlak) en dan met de muis sleept.
Zorg er verder voor dat het rechter zijvlak (als er op dat rechter zijvlak geklikt wordt en dan gesleept)
m.b.v. de muis naar rechts gedraaid kan worden, maar niet meer dan 180 graden.
En zorg er voor dat de figuur naar links bewogen kan worden (m.b.v. een schuifinvoervariabele).
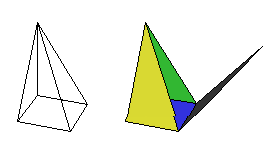
-
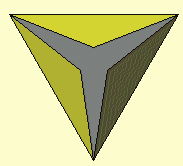
Maak een programma voor het tekenen van een driezijdige piramide (tetraeder), waarvan de zijvlakken en het grondvlak gelijkzijdige
driehoeken zijn met zijden van 100 mm, en waarvan de top loodrecht boven het middelpunt van het grondvlak ligt.
De top ligt 82 mm boven het grondvlak.
Het middelpunt van het grondvak (waar de top loodrecht boven ligt) ligt 58 mm van de hoekpunten, en op 29 mm afstand van de zijden.
De lengte van een hoogtelijn in het gondvlak is dus 87 mm.
Zorg er voor dat alle vier vlakken worden ingekleurd; het grondvlak grijs en de opstaande zijvlakken geel. Zorg
er voor dat de binnenkant van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als
een vlak wordt opengeklapt).
En zorg er voor dat de piramide om de vertikale lijn door de top kan draaien (m.b.v. animatie).
De zijvlakken kunnen m.b.v. een schuifinvoervariabele naar beneden draaien. Zorg er voor dat alle opstaande zijvlakken
tegelijk naar beneden draaien als je de schuif verplaatst, en zorg er voor dat ze niet verder kunnen draaien dan tot het grondvlak.
En zorg er voor de figuur te vergroten en te verkleinen is m.b.v. een invoervariabele. Die variabele kan van -10 tot 10 lopen, en
als de variabele bijvoorbeeld 4 is dan moeten de zijden 40% groter worden (dus ze moeten worden vermenigvuldigd met 1.4).
Aanwijzing:
De zijden van het viervlak geef ik aan met g. Dan is de lengte van de hoogtelijn in een zijvlak g/2*√3 en de hoogte van
het viervlak is g/3*√6
De projectie van de top op het grondvlak heeft de coördinaten (g/2,0,g/6*√3)
En in java is de opdracht om √3 te berekenen: Math.sqrt(3)
Het achtervlak draaien om de x-as is simpel, want de onderste zijde valt langs de x-as.
Het linker zijvlak draait niet om de x-as of y-as of z-as, en we hebben alleen de opdrachten xdraai, ydraai en zdraai.
Daarom moet je, voordat het linker zijvlak gedraaid wordt, eerst het assenstelsel draaien. En wel zo dat de zijde, waarom je draait,
dezelfde richting als de x-as of als de z-as heeft. Als je -60 graden om de y-as draait is de zijde, waarom je draait,
evenwijdig aan de x-as.
Daarna laat je het (gedraaide) linker zijvlak tekenen, en omdat de onderste zijde dan langs de x-as loopt
zijn de opdrachten daarvoor vrijwel netzo als voor het achtervlak. En zo ga je verder.
Je kunt de draaiing ook programmeren zonder gebruik te maken van xdraai, ydraai en/of zdraai. Dan moet je wel wat wiskunde gebruiken
om de coördinaten van de gedraaide punten te berekenen.
De zijden van het viervlak geef ik aan met g.
Als het linkerzijvlak een hoek h met het grondvlak maakt, dan zijn de opdrachten om dat linkerzijvlak te tekenen:
double p=h*Math.PI/180;
stap(g/4+Math.cos(p)*g/8*Math.sqrt(3),Math.sin(p)*g/2*Math.sqrt(3),g/4-Math.cos(p)*g/8*Math.sqrt(3));
stap(g/4-Math.cos(p)*g/8*Math.sqrt(3),-Math.sin(p)*g/2*Math.sqrt(3),g/2*Math.sqrt(3)-g/4+Math.cos(p)*g/8*Math.sqrt(3));
stap(-g/2,0,g/2*Math.sqrt(3));
(en daarvoor moet je nog weten dat de java-opdracht voor sin(h) is Math.sin(p), voor cos(h) is Math.cos(h), en voor voor arctan(h)
is Math.atan(h)
Verder is de beginhoek van h = Math.acos(1/3)*180/Math.PI;
Als hoek h in graden is gegeven dan is de hoek in radialen: h*Math.PI/180;
Bij de sinus en de cosinus van hoeken wordt in java ervan uitgegaan dat de hoeken in radialen worden gegeven)
-
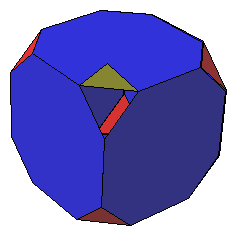
Maak een programma voor het tekenen van een kubus met ribben van 100 mm, waarvan de hoeken zijn afgezaagd.
De helft van de ribben zijn blijven staan, en aan beide kanten is er een kwart afgezaagd (zie de figuur hieronder).
Zorg er voor dat alle zes oorspronkelijke kubusvlakken worden ingekleurd met blauw,
en de afgezaagde vlakjes rood, op één na die geel is. De binnenkant
van de vlakken wordt met dezelfde kleur ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
Zorg er voor dat het gele vlakje kan worden gedraaid om één van de zijden, door op het vlakje te klikken
en de muis te verslepen.
Zorg er voor dat de kubus om de horizontale as (evenwijdig aan de y-as) in het midden van de kubus kan draaien (m.b.v. animatie).
En zorg er voor de figuur te vergroten en te verkleinen is m.b.v. een schuifinvoervariabele. Die variabele kan van 50 tot 150
lopen, en is in het begin 100.
Aanwijzing:
Je draait het driehoekje niet om de x-as of y-as of z-as, en we hebben alleen de opdrachten xdraai, ydraai en zdraai.
Daarom moet je, voordat er gedraaid wordt, eerst het assenstelsel draaien. En wel zo dat de zijde, waarom je draait, dezelfde
richting als de x-as of als de z-as heeft. Als je -45 graden om de y-as draait is de zijde, waarom je draait, evenwijdig aan de z-as.
Daarna laat je het (gedraaide) driehoekje tekenen. De opdracht om de bovenste zijde, waarom je draait, te tekenen is dan:
(en daarvoor moet je nog weten dat de java-opdracht voor √2 is: Math.sqrt(2) )
stap(0,0,g/4*Math.sqrt(2));
want die zijde loopt in de richting van de z-as en de lengte is (g/4)*√2, als g de lengte van de ribbe is.
De opdracht om de zijde in het rechterzijvlak te tekenen is dan
stap(g/8*Math.sqrt(2),-g/4,-g/8*Math.sqrt(2));
Je kunt de draaiing ook programmeren zonder gebruik te maken van xdraai, ydraai en/of zdraai. Dan moet je wel wat wiskunde gebruiken
om de coördinaten van de gedraaide punten te berekenen.
De ribben van de kubus geef ik aan met g (en de zijde van het driehoekje is dan : k = g * √2 / 4 )
Als het driehoekje over de hoek h gedraaid is, dan zijn de opdrachten om het driehoekje te tekenen:
double p=h*Math.PI/180;
stap(g/8+Math.cos(p)*g/8*Math.sqrt(3),Math.sin(p)*g/8*Math.sqrt(6),g/8-Math.cos(p)*g/8*Math.sqrt(3));
stap(g/8-Math.cos(p)*g/8*Math.sqrt(3),Math.sin(p)*-g/8*Math.sqrt(6),g/8+Math.cos(p)*g/8*Math.sqrt(3));
stap(-g/4,0,-g/4);
(en daarvoor moet je nog weten dat de java-opdracht voor sin(h) is Math.sin(p), voor cos(h) is Math.cos(h), en voor voor arctan(h)
is Math.atan(h)
Verder is de beginhoek van h = - Math.atan(Math.sqrt(2))*180/Math.PI;
Als hoek h in graden is gegeven dan is de hoek in radialen: h*Math.PI/180;
Bij de sinus en de cosinus van hoeken wordt in java ervan uitgegaan dat de hoeken in radialen worden gegeven)
-
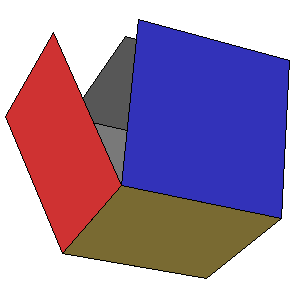
Maak een programma voor het tekenen van een kubus.
De ribben zijn 100 mm. Zorg er voor dat alle zes vlakken worden ingekleurd met verschillende kleuren, en dat de binnenkant
van de vlakken met dezelfde kleur is ingekleurd als de buitenkant (die binnenkant moet je zien als een vlak wordt opengeklapt).
Zorg er voor dat alle vlakken kunnen worden gedraaid, door op een vlak te klikken en de muis te verslepen.
Zorg er voor dat de kubus om de vertikale as in het midden van de kubus kan draaien, en dat je die draaiing kunt regelen met een
schuifinvoervariabele.
 Maak een programma voor de figuur hiernaast. Maak een programma voor de figuur hiernaast.
Hij bestaat uit driehoekjes en vierkanten. De zijden zijn 30. De hoeken van de driehoekjes zijn 60 graden.
De driehoekjes zijn rood, de vierkanten geel.
Begin met het vierkant linksmidden.
Verplaats dan de cursor naar het punt linksboven van het vierkant.
Teken dan de driehoek erboven. Verplaats dan de cursor naar het bovenste punt van de driehoek, en geef
hem de juiste richting voor het volgende vierkant.
Herhaal dat zes keer.
Zorg er vervolgens voor dat de figuur om het middelpunt draait.
|
| |
