Hoofdstuk 6 Programmeren in Pascal

6.5 Sorteren.

6.5.1. Sorteren

Bekijk de volgende lijst met namen

Je ziet natuurlijk dat de namen niet in alfabetische volgorde staan, ze zijn niet gesorteerd.
Als je ze wel gaat sorteren dan komt de lijst er als volgt uit te zien:

Er zijn verschillende manieren om de computer zo'n lijst met woorden of getallen te laten sorteren.
Dat worden sorteeralgoritmen genoemd.
Er wordt ontzettend veel computertijd gebruikt voor het sorteren van grote hoeveelheden gegevens, en daarom is het heel belangrijk om over goede sorteer-methoden te beschikken. In de afgelopen vijftig jaren zijn er veel sorteer-algoritmen ontwikkeld.
Wij gaan twee vrij eenvoudige methoden bekijken: het bubblesort-algoritme en het selectionsort-algoritme.

6.5.2. Het bubblesort-algoritme

De bubblesort-methode houdt in dat je steeds twee opeenvolgende woorden of getallen vergelijkt. Als die woorden of getallen in de juiste volgorde staan wordt er niets gedaan, maar anders worden ze omgewisseld. En daarmee ga je net zo lang door tot ze allemaal op de goede plaats staan.

Hier onder zie je een applet (gemaakt door Robert Lafore), waarin dat gedemonstreerd wordt.

New Genereert nieuwe data en initialiseert. De optie 'new' wisselt tussen random en aflopend.

Size Wisselt tussen 10 en 100 balkjes. Genereert ook nieuwe data en initialiseert.

Draw Tekent de balkjes opnieuw.

Run Start het automatisch sorteren (klik op 'Step' om te pauzeren en 'Run' om weer verder te gaan).

Step Voert één stap van het sorteerproces uit.

In het volgende voorbeeld demonstreren we het met de namen uit paragraaf 6.5.1.
Daarbij begin je met het laatste en één-na-laatste woord of getal, en daarna vergelijk je het één-na-laatste en het twee-na-laatste woord of getal, en zo ga je steeds verder naar voren.

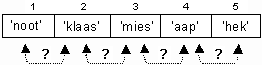
Als voorbeeld gaan we bij bovenstaande rij de woorden van achteren naar voren doorlopen, en zonodig steeds twee buur-woorden verwisselen.

Het vierde en vijfde woord staan in de juiste volgorde, die laten we dus staan.
Het derde en vierde woord staan in de verkeerde volgorde, die wisselen we dus om.

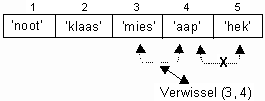
Het resultaat van deze Verwissel(3, 4)-bewerking zie je in de bovenste rij hier onder.
En ook hoe het verder gaat als je verder naar voren loopt.
Als je het eerste en tweede woord vergeleken hebt, en die eventueel verwisseld hebt, begin je weer bij de laatste twee. Zo ga je steeds verder.

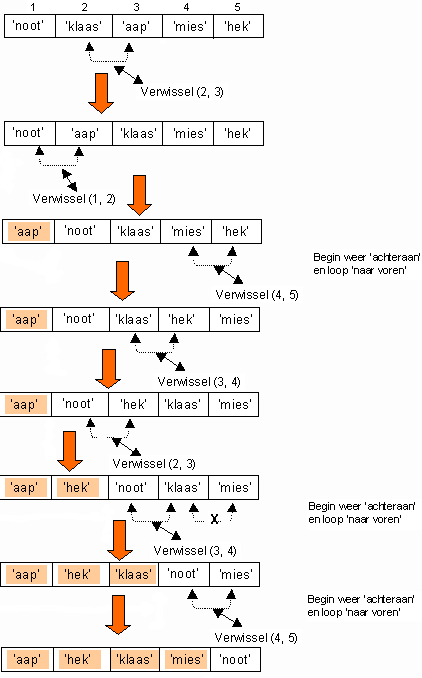
Bij deze aanpak wordt bij elke doorgang van achteren naar voren de kleinste waarde steeds naar voren geschoven. Na de eerste doorgang ben je er zeker van dat het eerste woord ook werkelijk vooraan staat.
Na de tweede doorgang ben je er zeker van dat het tweede woord ook werkelijk op de tweede plaats staat.
Als je de linkerkant als boven ziet (je moet de figuur eigenlijk een kwart slag rechtsom draaien), dan borrelen de lichtste waarden als het ware als luchtbelletjes naar boven, vandaar de naam bubblesort.
Je kunt zien, dat vanaf de linkerkant het gesorteerde deel van de rij toeneemt; dat gedeelte van de rij is met een kleurtje aangegeven.
Als er bij een bepaalde doorgang geen enkele verwisseling plaats vind is de rij gesorteerd, en dan is het klaar.

We zetten nu eerst in een structuurdiagram wat er in grote lijnen moet gebeuren:

Nu gaan we het eerste deelprobleem (namen invoeren) verfijnen.
We weten niet hoeveel namen er zullen worden ingevoerd, we gaan ervan uit dat er telkens een naam wordt ingevoerd. En als er op een gegeven moment, in plaats van het invoeren van een naam, direkt op enter wordt gedrukt (de naam is dan dus de lege string) nemen we aan dat er gestopt wordt met het invoeren van namen.
Dan moet dus het volgende gebeuren, in een structuurdiagram genoteerd:

Het tweede deelprobleem (sorteren) bestaat uit meer stappen als we het gaan verfijnen.
We gaan niet direkt tot in de finesses verfijnen, we doen het weer in etappes.
Eerst verfijnen we het als volgt:

Het deelprobleem: Maak een doorloop enz..... gaan we nu verder verfijnen.
In een structuurdiagram wordt dat het volgende:

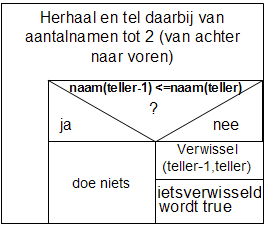
Het deelprobleem: Verwissel (teller-1, teller) moeten we ook nog in stapjes verdelen.
Als je de inhoud van twee variabelen a en b wilt verwisselen, dan kan dat niet met de opdrachten:
a := b;
b := a;
Want stel je voor dat a het woord mies bevat, en b het woord aap.
Dan zal na de opdracht a := b de variabele a het woord aap bevatten, en b bevat ook nog steeds het woord aap.
En dan ben je het woord mies kwijt!
En na de volgende opdracht b := a zal de variabele b het woord aap bevatten, en a bevat ook het woord aap.
Dan zijn ze dus niet verwisseld.
Je hebt een extra hulpvariabele nodig, waarin het eerste woord wordt bewaard.
Het moet als volgt:

hulp := b;
b := a;
a := hulp;

Het laatste deelprobleem (de gesorteerde lijst) kun je vast zelf wel verfijnen.

Nu gaan we het struktuurdiagram omzetten in een programma.
Van elke deelprobleem, dat we hebben verfijnd in een nieuw struktuurdiagram, maken we een procedure.
We voegen de header toe, en de declaraties. En dan krijgen we het volgende programma:

program bubblesort;

var aantal: integer;
   namen: array [1..100] of string;

procedure invoeren;
var naam: string;
   i: integer;
begin
   {de teller krijgt eerst de waarde 1}
   i:=1;
   {de variabele naam moet een (willekeurige) waarde krijgen
   want als naam gelijk is aan de lege string zal de  
   while-lus direkt stoppen}
   naam:="test";
   while naam<>"" do
   begin
      write("Geef naam nummer ",i:2,"        ");
      readln(naam);
      namen[i]:=naam;
      {voor het vervolg de letter met 1 ophogen}
      i:=i+1;
   end;
   {als er gestopt wordt is het aantal namen gelijk aan i-1}
   aantal:=i-1;
end;

procedure verwissel(var a:string; var b:string);
var hulp: string;
begin
   hulp:=a;
   a:=b;
   b:=hulp;
end;

procedure maakdoorloop(var ietsverwisseld:boolean);
var i: integer;
begin
   ietsverwisseld:=false;
   for i:=aantal downto 2 do
   begin
      if (namen[i-1]>namen[i] ) then
      begin
         verwissel(namen[i-1],namen[i]);
         ietsverwisseld:=true;
      end;
   end;
end;

procedure sorteer;
var ietsverwisseld: boolean;
begin
	repeat
	   maakdoorloop(ietsverwisseld)
	until (ietsverwisseld=false);
end;

procedure drukaf;
var i:integer;
begin
   writeln;writeln;writeln("de gesorteerde lijst:");
   for i:=1 to aantal do
   writeln(namen[i]);
end;


begin
   invoeren;
   sorteer;
   drukaf;
end.

en als we het programma dan uitvoeren kan het volgende verschijnen:

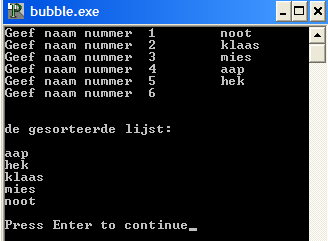
6.5.3. Het selectionsort-algoritme

Bij de selectionsort-methode zoek je eerst het kleinste element van de rij met woorden (of getallen) op. En dat kleinste element verwissel je dan met het eerste woord of getal van de rij.
Vervolgens zoek je het kleinste element vanaf het tweede woord (of getal) op. En dat kleinste element verwissel je dan met het tweede woord of getal van de rij.
En zo ga je steeds verder.
Steeds zoek je het kleinste element op van het nog ongesorteerde deel van de rij, en dat kleinste element verwissel je dan met het éérste element van het nog ongesorteerde deel van de rij.
Op die manier vergroot je het gesorteerde deel steeds met één element.

Je bent klaar als alles-min-één gesorteerd is, want als je bij de laatste twee bent aangekomen wordt de kleinste van die twee op de één na laatste plaats gezet, en dan staat de grootste dus automatisch achteraan.

Hier onder zie je een applet (gemaakt door Robert Lafore), waarin dat gedemonstreerd wordt.

In het volgende voorbeeld demonstreren we het met de namen uit paragraaf 6.5.1.
Je begint als volgt:

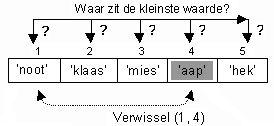
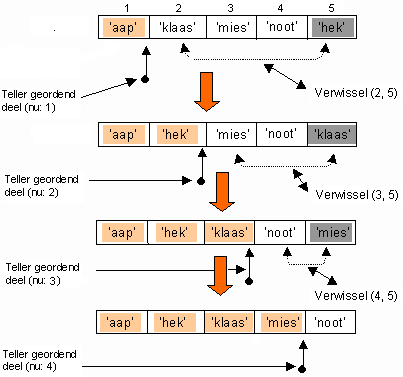
Het resultaat van deze Verwissel(1,4)-bewerking zie je in de bovenste rij hier onder.
En ook hoe het verder gaat.
Het donker gearceerde geeft steeds de volgende gevonden kleinste waarde aan.
Het oranje gearceerde geeft steeds de het al gesorteerde deel aan.

We zetten nu eerst in een structuurdiagram wat er in grote lijnen moet gebeuren, dat is eigenlijk het zelfde als in de vorige paragraaf:

De verfijning van het eerste deelprobleem (namen invoeren) en van het laatste deelprobleem (gesorteerde lijst afdrukken) gaat net zo als in de vorige paragraaf.
Het tweede deelprobleem (sorteren) gaan we ook nu niet direkt tot in de finesses verfijnen, we doen het weer in etappes.
Eerst verfijnen we het als volgt:

Het deelprobleem Zoek de kleinste vanaf teller gaan we nu verder verfijnen.
In een structuurdiagram wordt dat het volgende:

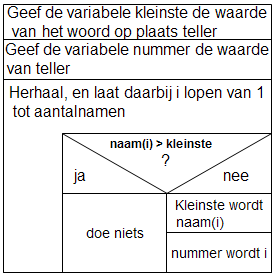
Het deelprobleem: Verwissel de kleinste met het woord op plaats teller hebben we in de vorige paragraaf al besproken.

Nu gaan we het struktuurdiagram omzetten in een programma.
Van elke deelprobleem, dat we hebben verfijnd in een nieuw struktuurdiagram, maken we weer een procedure.
We voegen de header toe, en de declaraties. En dan krijgen we het volgende programma:

program selectionsort;

var aantal: integer;
   namen: array [1..100] of string;

procedure invoeren;
var naam: string;
   i: integer;
begin
   {de teller krijgt eerst de waarde 1}
   i:=1;
   {de variabele naam moet een (willekeurige) waarde krijgen
   want als naam gelijk is aan de lege string zal de  
   while-lus direkt stoppen}
   naam:="test";
   while naam<>"" do
   begin
      write("Geef naam nummer ",i:2,"        ");
      readln(naam);
      namen[i]:=naam;
      {voor het vervolg de letter met 1 ophogen}
      i:=i+1;
   end;
   {als er gestopt wordt is het aantal namen gelijk aan i-1}
   aantal:=i-1;
end;

procedure verwissel(var a:string; var b:string);
var hulp: string;
begin
   hulp:=a;
   a:=b;
   b:=hulp;
end;

procedure zoekkleinste(teller:integer; var nummerkleinste: integer);
var i: integer;
    kleinste: string;
begin
   kleinste:=namen[teller];
   nummerkleinste:=teller;
   for i:=teller to aantal do
   begin
      if (namen[i]<=kleinste ) then
      begin
         kleinste:=namen[i];
         nummerkleinste:=i;
      end;
   end;
end;

procedure sorteer;
var i, nummerkleinste: integer;
begin
for i:=1 to aantal-1 do
   begin
      zoekkleinste(i,nummerkleinste);
      verwissel(namen[i],namen[nummerkleinste]);
   end;
end;

procedure drukaf;
var i:integer;
begin
   writeln;writeln;writeln("de gesorteerde lijst:");
   for i:=1 to aantal do
   writeln(namen[i]);
end;


begin
   invoeren;
   sorteer;
   drukaf;
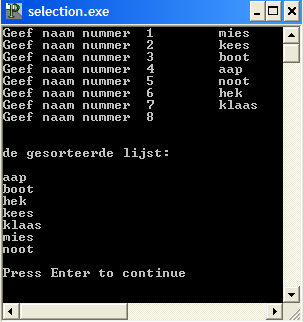
end.

en als we het programma dan uitvoeren kan het volgende verschijnen:

Opgaven.
Maak nu opgave 18 van hoofdstuk 6 (Pascal)