Informaticasite van het Lauwers College te Buitenpost © R.J. van der Beek

Menu
Opg/pres H1
Hoofdst 1
Hoofdst 2
Hoofdst 3
Hoofdst 4
H5
H6
H7
H8

Hoofdstuk 1. Digitaliseren

1.1 Bits, bytes en getallen

Een computer werkt alleen met nullen en enen, dat heb je vast wel eens gehoord.
Maar je merkt er niets van, je ziet gewone letters op het scherm, foto's, en nog veel meer. Hoe kan dat nu met alleen nullen en enen?
Dat gaan we in dit hoofdstuk uitleggen.

In een computer zitten miljoenen kleine schakelaars. Zo'n schakelaar kan twee posities aannemen: stroom doorlaten of juist niet.
En die twee mogelijkheden geven we aan met 1 en 0.
Zo'n schakelaar noemen we een bit, afgeleid van binary digit.
Binary betekent twee-tallig en digit komt van een grieks woord voor vinger. Als je klein bent gebruik je je vingers immers vaak bij het tellen.

Een bit kan dus twee waarden aannemen: 1 en 0

Als je twee bits gebruikt heb je vier verschillende combinaties: 00, 01, 10 en 11
Met drie bits zijn er acht combinaties: 000, 001, 010, 011, 100, 101, 110 en 111
Met vier bits kun je zestien combinaties maken: je kunt voor alle acht combinaties met drie bits een 0 zetten, maar ook kun je voor die acht combinaties een 1 zetten.
Elke keer als je een bit toevoegt krijg je twee keer zoveel combinaties.

Met 4 bits heb je dus 16 ( = 2 ⁴ ) mogelijkheden.
Met 5 bits heb je 32 ( = 2 ⁵ ) mogelijkheden.
Met 6 bits heb je 64 ( = 2 ⁶ ) mogelijkheden.
Met 7 bits heb je 128 ( = 2 ⁷ ) mogelijkheden.
Met 8 bits heb je 256 ( = 2 ⁸ ) mogelijkheden.
Met 10 bits heb je 1024 ( = 2 ¹⁰ ) mogelijkheden.
Met 16 bits heb je 65536 ( = 2 ¹⁶ ) mogelijkheden.

Bits worden meestal in groepjes van acht bij elkaar genomen, dat noemen we een byte (dat is de samentrekking van by eight).
Een byte kan 256 ( = 2 ⁸ ) verschillende waarden hebben.

De grootte van bestanden of de omvang van het geheugen wordt meestal gegeven in kilobytes of megabytes of gigabytes.
Een kilobyte, afgekort kB, is 1000 bytes. Vaak wordt gezegd dat een kilobyte 1024 bytes ( = 2 ¹⁰ ) is, maar officieel wordt dit nu een kibibyte genoemd, afgekort KiB.
De volgende benamingen worden gebruikt:

kB (kilobyte)	1000¹ = 10³	KiB (kibibyte)	2¹⁰ = 1024¹
MB (megabyte)	1000² = 10⁶	MiB (mebibyte)	2²⁰ = 1024²
GB (gigabyte)	1000³ = 10⁹	GiB (gibibyte)	2³⁰ = 1024³
TB (terabyte)	1000⁴ = 10¹²	TiB (tebibyte)	2⁴⁰ = 1024⁴

1.2 Getalstelsels

Er zijn verschillende getalstelsels, en in de computerwereld wordt meestal met een speciaal getalstelsel gewerkt.

Romeinse getallen zie je wel op oude gebouwen, waarop dan staat aangegeven wanneer het gebouwd is.
Daarbij worden de letters I, V, X, enz. gebruikt. Die letters hebben een bepaalde waarde:
I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000

Als er meerdere letters gebruikt worden moet je die gewoon bij elkaar optellen.
Behalve als er een letter met een grotere waarde achter staat, dan moet je de waarde er van aftrekken.
Dus:

II = 2
III = 3
IV = 4
VI = 6
VII = 7
VIII = 8
IX = 9
XX = 20
XXX = 30
XL = 40
MMCMLXVI = 2966

Een nadeel van deze notatie is dat je erg lange en onoverzichtelijke getallen krijgt.

In ons decimale of tientallige getalstelsel gebruiken we maar 10 symbolen (cijfers) namelijk 0, 1, 2, 3, 4, 5, 6, 7, 8 en 9.
De waarde die de cijfers hebben hangt af van hun plaats, bijvoorbeeld:
3847 = 7 + 40 + 800 + 3000 = 7 + 4 x 10¹ + 8 x 10² + 3 x 10³

In de computerwereld wordt meestal gewerkt met het binaire of tweetallige getalstelsel. Daarin worden maar twee tekens gebruikt, namelijk 0 en 1.
Omdat een bit maar twee waarden kan aannemen, namelijk 0 en 1, is het tweetallig getalstelsel het voor de hand liggende systeem voor de computer.

In het tientallig stelsel moet je een getal van achter naar voren lezen. Het laatste cijfer blijft gelijk, het cijfer daarvoor moet keer 10, het cijfer daarvoor moet keer 100 (=10²), het cijfer daarvoor moet keer 1000 (=10³), enz.
In het binaire getalstelsel moet je een getal ook van achter naar voren lezen. Het laatste cijfer blijft weer gelijk, het cijfer daarvoor moet keer 2, het cijfer daarvoor moet keer 4 (=2²), het cijfer daarvoor moet keer 8 (=2³), enz.

De decimale waarde van een binair getal kun je dus op de volgende manier bepalen:

101 = (van achter naar voor) 1 + 0 x 2 + 1 x 4 = 5
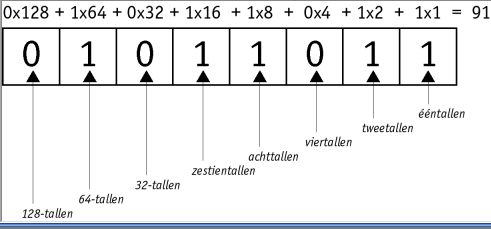
11011010 = 0 + 1 x 2 + 0 x 4 + 1 x 8 + 1 x 16 + 0 x 32 + 1 x 64 + 1 x 128 = 2 + 8 + 16 + 64 + 128 = 208
11111111 = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255, en dat is het grootste getal dat met een byte is te maken!

Hoe maak je van een decimaal getal een binair getal?

Je kijkt eerst wat de grootste macht van 2 is die kleiner of gelijk aan je getal is.
Die macht van 2 trek je van je getal af, en dan ga je op dezelfde manier verder met de rest.

Neem bv 29
16 is een macht van 2 (16 = 2⁴) en kleiner dan 29, de volgende macht (32 = 2⁵)) is te groot.
29 - 16 = 13. De grootste macht van 2 kleiner of gelijk 13 is 8 (8 = 2³).
13 - 8 = 5. de grootste macht van 2 kleiner of gelijk 5 is 4 (4 = 2²)
5 - 4 = 1
dus 29 = 16 + 8 + 4 + 1 = 2⁴ + 2³ + 2² + 2⁰
binair is dat dus 11101

Een andere manier werkt als volgt:
Deel het getal steeds door 2 (totdat de uitkomst 0 is) en schrijf de rest op (die kan dus 0 of 1 zijn)
Schrijf daarna de resten achter elkaar (achterstevoren) op, en je hebt de uitkomst.

Voorbeeld (we nemen weer 29)
29 delen door 2 is 14, rest 1
14 delen door 2 is 7, rest 0
7 delen door 2 is 3, rest 1
3 delen door 2 is 1, rest 1
1 delen door 2 is 0, rest 1

De resten in omgekeerde volgorde geven het binaire getal: 11101

Nog een voorbeeld: 205
205 is kleiner dan 256, dus het is in één byte (dus 8 bits) te schrijven.
De machten van twee die daarin voorkomen zijn 128, 64, 32, 16, 8, 4, 2 en 1
205: zit 128 er in? Ja, schrijf een 1 op.
205 - 128 = 77
77: zit 64 er in? Ja, schrijf een 1 op.
77 - 64 = 13
13: zit 32 er in? Nee, schrijf een 0 op.
13: zit 16 er in? Nee, schrijf een 0 op.
13: zit 8 er in? Ja, schrijf een 1 op.
13 - 8 = 5
5: zit 4 er in? Ja, schrijf een 1 op.
5 - 4 = 1
1: zit 2 er in? Nee, schrijf een 0 op.
1: zit 1 er in? Ja, schrijf een 1 op.
1 - 1 = 0, klaar

Dus 205 (decimaal) = 11001101 (binair)

Naast het binaire en het decimale getalstelsel wordt in de informatica ook nog het hexadecimale of zestientallige getalstelsel gebruikt.
In het zestientallige of hexadecimale getalstelsel worden zestien tekens (cijfers genoemd) gebruikt. Naast de cijfers 0 t/m 9 worden ook de hoofdletters A t/m F gebuikt, met als waarden 10 t/m 15.

decimaal	hexadecimaal	binair
0	0	0
1	1	1
2	2	10
3	3	11
4	4	100
5	5	101
6	6	110
7	7	111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111
16	10	1 0000
17	11	1 0001
18	12	1 0010
19	13	1 0011
20	14	1 0100

In het hexadecimale getalstelsel lees je een getal, net zo als bij een binair en decimaal getal, ook van achter naar voren. Het laatste cijfer blijft weer gelijk, het cijfer daarvoor moet keer 16, het cijfer daarvoor moet keer 256 (=16²), enz.
In de informatica worden eigenlijk alleen maar hexadecimale getallen van twee cijfers gebruikt.

Voorbeelden:

35 (hexadecimaal) = 3 x 16 + 5 = 53 (decimaal)
4B (hexadecimaal) = 4 x 16 + 11 = 75 (decimaal)
A7 (hexadecimaal) = 10 x 16 + 7 = 167 (decimaal)
BD (hexadecimaal) = 11 x 16 + 13 = 189 (decimaal)
FF (hexadecimaal) = 15 x 16 + 15 = 255 (decimaal), dus het grootste hexadecimale getal van twee cijfers is 255.
En dat is ook het grootste binaire getal van 8 bits, dus een byte. Dat is ook de reden dat hexadecimale getallen veel gebruikt worden in de informatica: getallen die in een byte passen zijn met twee tekens te schijven in het hexadecimale getalstelsel.

Hoe maak je van een decimaal getal (kleiner dan 256) een hexadecimaal getal?

Deel het getal door 16
Schrijf het getal dat er uitkomt op, en de rest er achter.
Maar denk er om dat als de uitkomst of de rest groter dan 9 is, je 10 moet vervangen door A, 11 door B, 12 door C, 13 door D, 14 door E en 15 door F.

Neem bv 199
199 gedeeld door 16 is 12, en de rest is 7
Vervang 12 door C, dan is het antwoord dus C7

Hexadecimale getallen kom je bijvoorbeeld tegen in HTML-documenten, bij het aangeven van kleuren.
Met bgcolor="#FF0098" geef je aan wat de achtergrondkleur van de webpagina is.
Je moet dan FF0098 verdelen in drie groepjes van 2: FF geeft aan wat de hoeveelheid rood is, maar dan als hexadecimaal getal, 00 geeft aan geeft aan wat de hoeveelheid geel is en 98 geeft de hoeveelheid blauw als hexadecimaal getal.

1.3 Binaire getallen optellen

Je hebt op de basisschool geleerd hoe je grote decimale getallen moet optellen.
Je zet ze onder elkaar, en dan begin je achteraan.

Neem bijvoorbeeld 538 + 764
Begin met 8 + 4, dat is 12, dus 2 opschrijven en 1 onthouden.
Dan 1 (onthouden) + 3 + 6, dat is 10, dus 0 opschrijven en 1 onthouden.
Tenslotte 1 (onthouden) + 5 + 7, dat is 13, dat opschrijven.
Dus 538 + 764 = 1301

Binaire getallen tel je op dezelfde manier op. Maar dan moet je er om denken dat je alleen nullen en enen mag gebruiken.
Dus 1 + 1 is 2, maar dat schrijf je binair als 10
En 1 + 1 + 1 is 3, maar dat schrijf je binair als 11

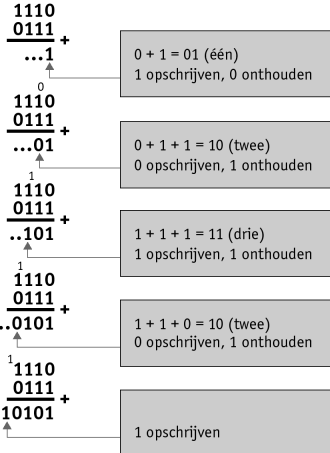
Nog een voorbeeld 10111011 + 01010101
Begin achteraan met 1 + 1, dat is 10 (geen 2!), dus 0 opschrijven en 1 onthouden.
Dan de op één na laatste: 1 (onthouden) + 1 + 0, dat is 10, dus 0 opschrijven en 1 onthouden.
Dan de op twee na laatste: 1 (onthouden) + 0 + 1, dat is 10, dus 0 opschrijven en 1 onthouden.
Dan de op drie na laatste: 1 (onthouden) + 1 + 0, dat is 10, dus 0 opschrijven en 1 onthouden.
Dan de op vier na laatste: 1 (onthouden) + 1 + 1, dat is 11, dus 1 opschrijven en 1 onthouden.
Dan de op vijf na laatste: 1 (onthouden) + 1 + 0, dat is 10, dus 0 opschrijven en 1 onthouden.
Dan de op zes na laatste: 1 (onthouden) + 1 + 0, dat is 10, dus 0 opschrijven en 1 onthouden.
Tenslotte de voorste: 1 (onthouden) + 1 + 0, dat is 10, dus 10 opschrijven.
Dus 10111011 + 01010101 = 10001000

Bij het voorbeeld hierboven zag je dat er twee bytes werden opgeteld. Het antwoord bestond uit 9 bits, en past dus niet in een byte.
Als er gewerkt wordt met getallen van een byte dan levert dat een probleem op, dat wordt overflow genoemd.
Een programma werkt vaak met een vast aantal bytes voor gehele getallen. Meestal wordt er meer dan één byte voor een getal gebruikt, want anders kunnen er geen getallen groter dan 255 worden gebruikt. Vaak worden er 4 bytes voor getallen gebruikt. Als er dan twee getallen worden opgeteld, en het resultaat past niet in 4 bytes, dan volgt er een foutmelding en dan heb je overflow.

1.4 Negatieve getallen in het binaire getalstelsel

Negatieve getallen moeten ook met alleen nullen en enen worden weergegeven, want een bit kan alleen 1 of 0 zijn en dus geen min.
Natuurlijk zou je kunnen afspreken dat als het eerste bit van een getal een 1 is, dat het dan een min voorstelt, en als het met een 0 begint het een positief getal is. Maar dat blijkt in de praktijk niet handig te zijn.
Er wordt gebruik gemaakt van de 2-complement methode.
Die methode is er op gebaseerd dat als je een positief en een negatief getal optelt, die absoluut genomen (zonder naar de + of - te kijken) gelijk zijn, er 0 uitkomt.

De methode werkt als volgt:
Als je een positief binair getal hebt, en je wilt het negatieve getal dat absoluut genomen even groot is, dan ga je alle bits omdraaien (enen in nullen veranderen en nullen in enen) en daarna er 1 bij optellen. Het getal dat je dan krijgt is het gevraagde negatieve getal.

Neem aan dat we werken met getallen van twee bytes, en neem bijvoorbeeld het getal 0011101101010101
Draai alle bits om, dan krijg je 1100010010101010
Tel er 1 bij op, dan krijg je 1100010010101011. En dat is het gevraagde getal.

Als je namelijk 0011101101010101 en 1100010010101011 optelt, dan krijg je 10000000000000000.
Maar dat past niet in twee bytes.
De computer laat daarom het voorste bit weg en dan heb je 0000000000000000, dus 0

Dit heeft tot gevolg dat er ook een gemakkelijke methode te bedenken is voor de computer om getallen van elkaar af te trekken.
Als de computer bijvoorbeeld 25 en 17 van elkaar af moet trekken dan gaat hij er een optelling van maken: hij telt 25 en -17 bij elkaar op!

1.5 Schakelaars in de computer

In een computer is een bit eigenlijk een schakeling, die open en dicht kan staan.
Zo'n schakelaar heet ook wel een transistor. Er zitten miljoenen transistoren op een chip van een vierkante centimeter.
Schakelaars kunnen met elkaar verbonden worden door middel van een schakeling, en zo'n schakeling kan er voor zorgen dat een andere schakelaar in een bepaalde stand komt te staan.
Je kunt daarbij denken aan lichtschakelaars, die aan of uit kunnen staan, en die zijn dus te vergelijken met een bit.
Je kunt ook denken aan een lamp, die aan of uit kan staan, en die dus ook te vergelijken is met een bit.

Je hebt verschillende soorten schakelingen.
Bekijk de schakeling hieronder maar eens, dat is de zogenaamde en-schakeling.

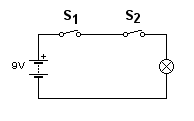
S1 en S2 zijn schakelaars, en het rondje met het kruisje er in stelt een lamp voor. Verder zie je een voeding.
Bij deze schakeling brandt de lamp alleen als schakelaar 1 en schakelaar 2 beide gesloten zijn, dus aan staan.
Daarom wordt dit wel een en-schakeling genoemd, of in het engels een AND-poort.
We kunnen de mogelijke standen van de schakelaars S1 en S2 met de gevolgen voor de lamp in een tabel weergeven:

S1	S2	X (lamp)
0	0	0
0	1	0
1	0	0
1	1	1

Behalve de AND-poort is er ook een OR-poort (Nederlands: OF-schakeling).
Die ziet er als volgt uit:

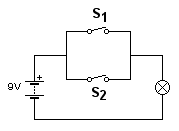
S1 en S2 zijn weer schakelaars, en het rondje met het kruisje er in is weer een lamp.
Bij deze schakeling brandt de lamp als schakelaar 1 of schakelaar 2 gesloten is (of allebei).
De tabel die hierbij hoort ziet er als volgt uit:

S1	S2	X (lamp)
0	0	0
0	1	1
1	0	1
1	1	1

Tenslotte is er nog de XOR-poort (Nederlands: XOF-schakeling).
Die ziet er als volgt uit:

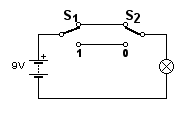
S1 en S2 zijn weer schakelaars. S1 staat aan als de schakelaar naar beneden staat (daarom staat bij de onderkant een 1) en S2 staat aan als de schakelaar naar boven staat (daarom staat bij de onderkant een 0).
Bij deze schakeling brandt de lamp als schakelaar 1 of schakelaar 2 aan is, maar niet allebei; daarom wordt wel het exclusieve of genoemd, en daarom staat er een X voor het woordje of (de x van exclusief).
Dit wordt ook wel een hotel-schakeling genoemd. Vrijwel elk huis met een trap heeft zo'n schakeling voor het traplicht. Het licht kan bediend worden met twee schakelaars, één voor onder en één voor boven.
De tabel die hierbij hoort ziet er als volgt uit:

S1	S2	X (lamp)
0	0	0
0	1	1
1	0	1
1	1	0

Er zijn speciale symbolen voor de logische poorten ontworpen door de Amerikaanse defensie. Later zijn er ook internationale afspraken gemaakt voor dit soort symbolen, maar de Amerikaanse militaire symbolen worden toch nog heel vaak gebruikt. Je ziet ze hier onder.

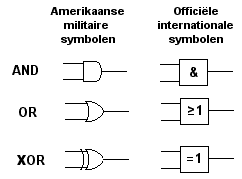
Met behulp van logische schakelingen kun je eenvoudige optellingen van bits maken. Kijk eerst naar het optellen van twee 1-bits getallen.

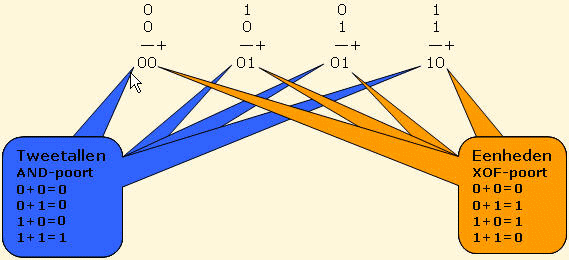
Wanneer je de uitkomst van bovenstaande sommetjes vergelijkt met de tabellen van de verschillende poorten, dan blijkt dat de eenheden (het achterste bit van de uitkomst) bepaald worden door een XOF-poort en de tweetallen (het voorste bit van de uitkomst) door een AND-poort.
Met behulp van een AND- en XOF-poort kun je dus een 'Een-Bit-Opteller' bouwen. Deze schakeling wordt ook wel een 'Half Adder' genoemd, zie hier onder.

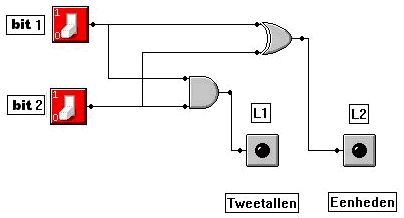
Een 'Half Adder'-schakeling is dus een belangrijke elektronische component die gebruikt wordt bij het optellen van bits. De schakelingen worden een stuk ingewikkelder als er grotere getallen moeten worden opgeteld.
In paragraaf 1.3 is uitgelegd hoe je zelf grotere binaire getallen kunt optellen: je begint dan met de achterste bits en dan werk je naar voren, en je moet steeds kijken wat je moet onthouden.

Als je een schakeling wilt maken voor de optelling van grotere getallen, bijvoorbeeld van twee bytes, dan moet de computer het op dezelfde manier doen, dus ook steeds iets onthouden.

Wat er moet worden onthouden voor de optelling van de volgende bits (of beter gezegd: de vorige, want je werkt van achter naar voren) noem je de carry-out.

De schakeling die je nodig hebt om dit probleem op te lossen is de 'Full Adder'-schakeling. Deze schakeling zorgt er voor dat er drie bits worden opgeteld: de twee bits van de twee getallen en de carry-in.

Een 'Full Adder'-schakeling ziet er als volgt uit:

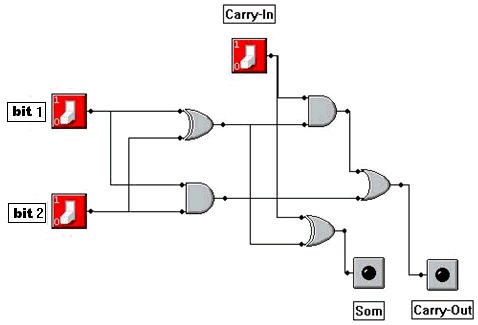
Carry-in is het onthouden van de vorige optelling en carry-out is het onthouden voor de volgende optelling.

Een 'Full Adder'-schakeling is dus een schakeling die als onderdeel gebruikt wordt bij een schakeling voor het optellen van binaire getallen die bestaan uit meer dan 1 bit.
Hier onder zie je dan de schakeling voor het optellen van twee getallen die beide uit 2 bits bestaan : de 'Twee Bits Teller'.

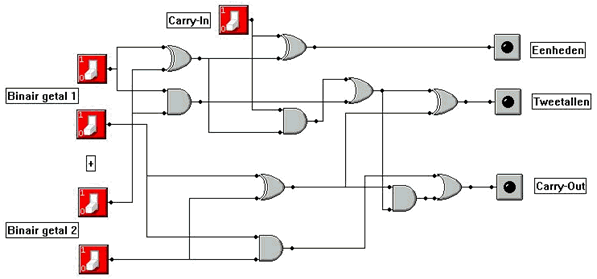
1.6 Digitaliseren en ASC-code

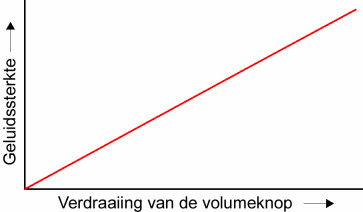
Een versterker in een geluidsinstallatie heeft een geluidsknop waarmee je de muziek harder en zachter kunt zetten.
Meestal is dat een draaiknop, en als je die langzaam rechtsom draait wordt de muziek steeds luider: er is een glijdend verloop van de geluidssterkte, het gaat niet met horten en stoten.
Zo'n glijdende schaal heet continu.
Je kunt het in een grafiek uitzetten zoals hier onder.

Er zijn ook veel versterkers die een geluidsknop hebben waar je steeds op klikken moet, en elke keer als je er op klikt wordt de muziek een beetje luider.
Het veranderen van de geluidssterkte verloopt dan in stappen, en dat noem je discreet. Je kunt het in een grafiek uitzetten zoals hier onder.

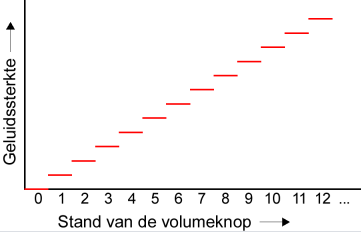
Een discrete schaal is dus een getrapte schaal. En de standen daarvan kun je gemakkelijk digitaliseren, je nummert de standen bijvoorbeeld van 0 tot 15.
Digitaliseren betekent dat je iets met behulp van bits (= binary digit, en digit zit ook in digitaal) vastlegt zodat het met de computer verwerkt kan worden.
Een discrete schaal kun je dus gemakkelijk digitaliseren, bij een continue schaal is dat lastiger.
Bij een continue schaal ga je dan het verloop ook in stapjes verdelen, en als je het dan maar in genoeg stapjes verdeelt zal het in de praktijk niet veel uitmaken of je een continue of een discrete schaal hebt.

Tekst digitaliseren

Tekst kan gedigitaliseerd worden door elk teken een bepaald nummer te geven.
Er is een afspraak gemaakt over die nummering, zodat iedereen dezelfde nummering gebruikt, dat is geregeld door de ISO (International Organization for Standardization). Die organisatie heeft een heleboel afspraken geregeld, ook over natuurkundige eenheden, enz. Dat noem je standaardisering.
Die standaard nummering staat in een tabel die de ASCII-tabel wordt genoemd. ASCII staat voor American Standard Code for Information Interchange.
Toen de ASC-code werd afgesproken werden er 7 bits gebruikt voor de codering, zodat er maar 128 verschillende tekens konden worden gecodeerd.
Dat bleek genoeg te zijn voor de tekens uit het standaard Engels en de andere symbolen die op een toetsenbord aanwezig zijn.
Maar andere talen maken van andere tekens gebruik, daarom werden er 8-bits ASCII-tabellen gemaakt zodat er 256 tekens konden worden gecodeerd.
Dat noemde men onder DOS Extended ASCII, en bij Windows de ANSI-code (American National Standards Institute), maar die twee zijn jammergenoeg niet gelijk.
Er bestaat dus geen standaard voor die laatste 128 tekens, maar voor de eerste 128 gelukkig wel.
De eerste 32 tekens van standaard ASCII zijn zogenaamde stuurtekens, en die worden meestal met een afkorting aangeduid.

Een paar bekende zijn: 10 = LF (dat is de afkorting van Line Feed: de cursor gaat een regel omlaag)
13 = CR (Carriage Return, de cursor gaat naar het begin van de regel)
7 = BELL (je hoort een piepje) 27=ESC

Wanneer woorden door een computer worden gesorteerd, gebeurt dit volgens het ASCII alfabet.
Dus hoofdletters vóór kleine letters, en kleine letters staan voor geaccentueerde letters, en de spatie komt allereerst.

Als je onder windows een teken nodig hebt dat niet op het toetsenbord staat, dan kun je dat krijgen door op het numerieke toetsenbord de decimale ASCII-code in te tikken, terwijl je de Alt-toets ingedrukt houdt.
Je krijgt dan een teken uit de Extended ASCII tabel, maar als je de ASCII-code laat voorafgaan door een 0 krijg je de ANSI code.

Elk teken heeft dus een ASC-code, dat is een getal tussen 0 en 255, en er wordt dus één byte per teken gebruikt.
Hier onder zie je de 256 ANSI-codes, en de eerste 128 zijn tegelijk ook de ASC-codes met de bijbehorende tekens.
Daaronder zie je de Extended ASCII tabel (die tabellen hoef je natuurlijk niet uit je hoofd te leren)

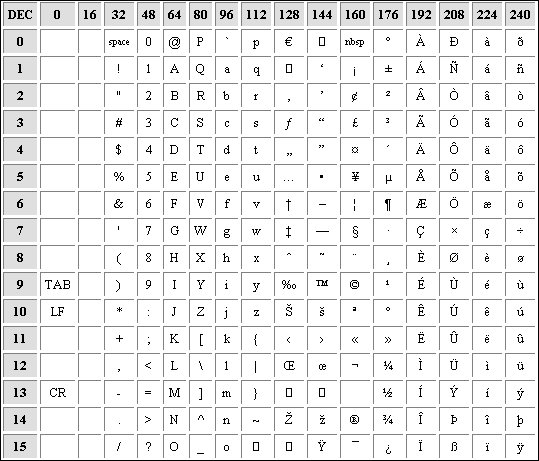
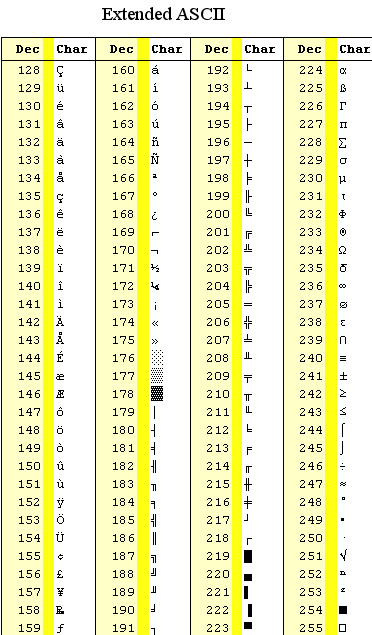
Je kunt het programma ASC.EXE gebruiken om te bekijken hoe een tekst door de computer wordt opgeslagen.
Je kunt dat programma hier downloaden.
Start het programma Kladblok, en tik het volgende in:
ABC abc
:!é
€

Sla het op (bijvoorbeeld onder de naam asc.txt)
Start dan het programma ASC, klik op Bestand Openen, en open het bestand asc.txt dat je net met Kladblok hebt gemaakt.
Dan zie je hoe de computer het heeft opgeslagen, zie de figuur hieronder.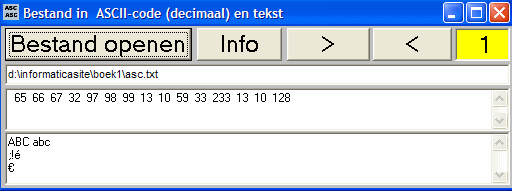
Je ziet dan dat de A als het getal 65 is opgeslagen, B als 66, C als 67, de spatie als 32, de a als 97, de b als 98 en de c als 99
Dan zie je de getallen 13 en 10, en die zie je later nog eens.
Als er op de entertoets wordt gedrukt dan codeert Kladblok dat met de getallen 13 en 10 (13 is CR, dat staat voor cariage return, en dat betekent: ga naar het begin van de regel. En 10 is LF, dat staat voor line feed, en dat betekent: ga naar de volgende regel)
De puntkomma wordt als het getal 59 opgeslagen, het uitroepteken als 33 en de é als 233
Dan zie je de getallen 13 en 10 weer, die staan voor de entertoets.
En tenslotte zie je dat het euroteken als het getal 128 wordt opgeslagen.

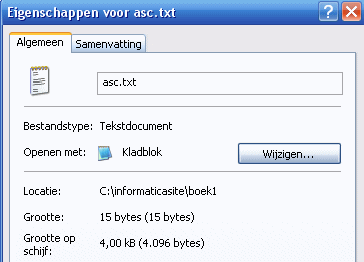
Als je naar de Verkenner gaat, en rechtsklikt op het bestand asc.txt, dat je net gemaakt hebt, dan krijg je een snelmenu.
En als je in dat menu klikt op eigenschappen dan krijg je te zien uit hoeveel bytes het bestand bestaat.
Dat zijn er 15. Want je hebt 11 gewonen tekens ingetikt, en twee keer de entertoets (die geeft 2 codes, dus 2 bytes). Je ziet dan het volgende:

1.7 UNI-code

Met de ASC-code kunnen maar 255 tekens worden gecodeerd, er wordt dan 1 byte per teken gebruikt.
Maar er zijn veel meer dan 255 tekens.
Daarom wordt ook de uni-code gebruikt. Daarmee kunnen meer dan 64000 tekens worden gecodeerd, er worden dan 2 bytes per teken gebruikt.

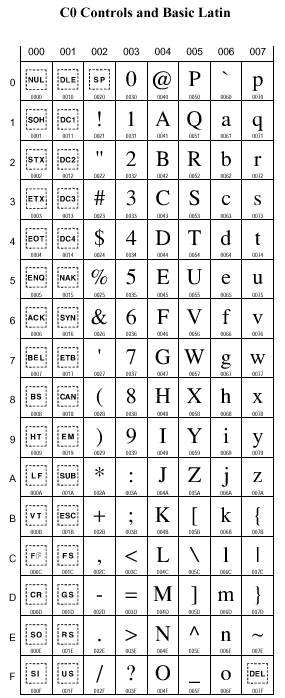
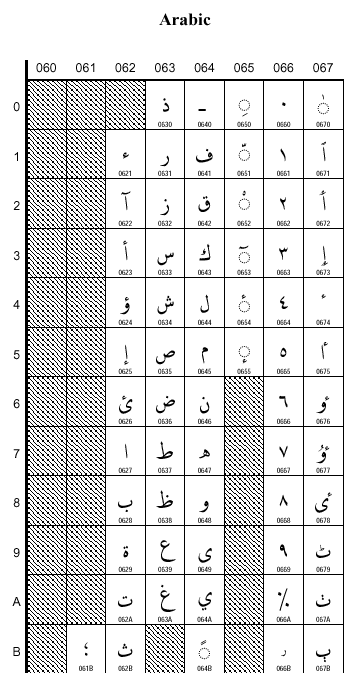
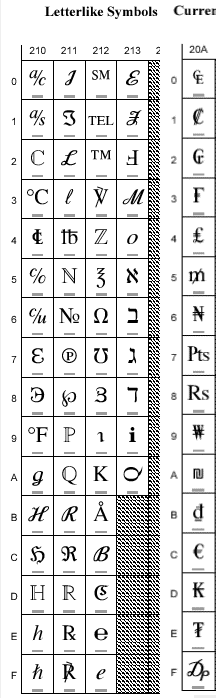
Hieronder zie je een aantal van die 64000 tekens met de bijbehorende uni-code.
Die uni-code wordt in deze tabellen met hexadecimale getallen aangegeven.
Als je bijv. in onderstaande tabel (links) naar de A kijkt dan zie je dat er 004 boven staat en een 1 voor. Dat betekent dat de hexadecimale code van de A 0041 is.
En decimaal is dat 1 + 4 x 16 = 65. Dat is hetzelfde als de ASC-code van de A.
De unicode-tekenset bevat dus ook de asccode-tekenset, en de codes zijn voor die tekens gelijk.

1.8 RGB

Een kleur kan worden gemaakt door bepaalde hoeveelheden van de drie basiskleuren rood , groen en blauw te mengen.
Als je een kleur op die manier met de computer maakt wordt het een RGB-kleur genoemd.
Je kunt onderstaand applet gebruiken om te bekijken welke kleur je krijgt als je bepaalde hoeveelheden rood, groen en blauw mengt.
Je kunt de rgb-kleuren instellen met behulp van de rode schuifjes.

Onder de schuifbalk zie je een getal, dat de hoeveelheid licht van die kleur aangeeft.
Dat is een getal tussen 0 en 255, dat kan dus m.b.v. één byte.
Voor een complete RGB-kleur heb je dus drie bytes nodig, één voor elk van de drie basiskleuren.
Fel rood krijg je door de waarde voor rood maximaal (255) te zetten en de andere kleuren op 0. Probeer maar eens.
Fel groen krijg je door groen op 255 te zetten en de rest op 0.
De kleur geel is een mengsel van rood en groen.
Die kleur krijg je door rood en groen beide op 255 te zetten, en blauw op 0 Proberen maar.
Paars is een mengsel van rood en blauw, zet dus rood en blauw beide op 255, en groen op 0
Zwart krijg je door alle kleuren op 0 te zetten en wit door alle kleuren op 255 te zetten.
En grijs krijg je door gelijke hoeveelheden rood, groen en blauw te mengen. Hoe kleiner die getallen zijn hoe donkerder het wordt. Proberen maar.

1.9 Afbeeldingen digitaliseren: het bmp-formaat

De foto hieronder bestaat uit een groot aantal vierkantjes, die elk één bepaalde kleur hebben.
Die vierkantjes worden pixels genoemd, het woord pixel komt van picture element.
Normaal zie je die vierkantjes niet, maar als je de foto heel veel gaat uitvergroten kun je ze wel zien.

We hebben ingezoomd op een stukje van deze foto, dan zie je de afzonderlijke pixels.

Een foto als deze bestaat uit heel veel pixels en zal daarom veel bytes in beslag nemen, als er geen compressie plaats vindt.

Deze foto is ongeveer 400 bij 300 pixels, dat is 120.000 pixels.
Iedere pixel heeft een kleur en voor een kleur zijn 3 bytes nodig.
Voor de hele foto zijn dus 3 x 120.000, dat is 360.000 bytes nodig.
Als het als een bmp-file wordt opgeslagen worden er nog 54 bytes toegevoegd met algemene kenmerken van de figuur (bijvoorbeeld de lengte en de breedte).
Verder wordt aan het eind van elke rij met RGB-waarden van de pixels nog een nul aan het bestand toegevoegd.
In totaal bestaat het bmp-bestand van een foto van 400 bij 300 dus uit 360354 bytes: 360000 voor de 120000 pixels, 54 met algemene informatie en 300 nullen aan het eind van elke rij.

Een pagina tekst bevat hooguit 3000 tekens, dat is 3000 bytes.
Een foto zoals deze neemt dus evenveel ruimte in beslag als zo'n 120 pagina's tekst!

De fijnheid van de verdeling van de pixels noem je de resolutie. De resolutie van je beeldscherm kun je bijvoorbeeld instellen op 800 x 600, dan heb je 800 pixels in de breedte en 600 in de hoogte. Je kunt het bijvoorbeeld ook instellen op 1280 x 1024, dan worden de figuren kleiner dan bij 800 x 600 want je hebt meer pixels in beeld.
Bij printers wordt de resolutie van het printen aangegeven in dotch per inch (dpi), dat kan bijvoorbeeld 300 dpi zijn.

1.10 Paint

In tekenprogramma's en software voor bewerking van foto's kun je zelf kleuren instellen.

Start PAINT op (Klik op Start, dan op Programma's, dan op Bureauaccessoires, dan op Paint)
Dubbelklik op een kleur van het kleurenpalet. Dan krijg je een venster voor extra kleuren. Klik daarin op Aangepaste kleuren definiëren.

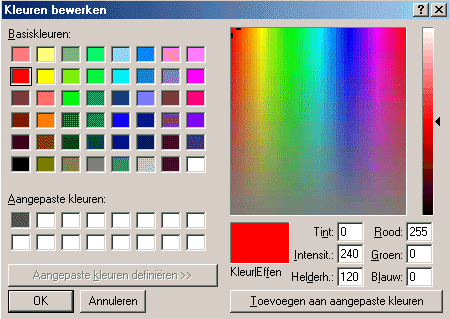
In het rechterdeel van het venster kun je kleuren instellen. (dit rechterdeel verschijnt pas nadat je op "Aangepaste kleuren definiëren" hebt geklikt)
Dit kan direct door het klikken op het regenboogvlak, maar je kunt ook direct waarden voor rood, groen en blauw invoeren. Dit kan in de vakjes rechtsonder.
De gekozen kleur zie je in het vlak met het bijschrift "Kleur | Effen".
Links van de drie waarden voor rood groen en blauw, staan drie andere: Tint, Intensiteit en Helderheid of in het engels: Hue, Saturation en Luminance.
Deze drie getallen vormen samen een andere manier om kleuren te beschrijven.
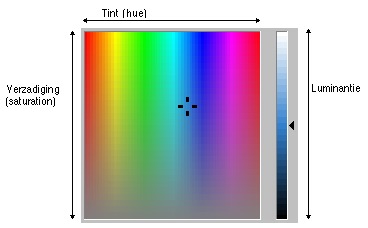
- Hue betekent tint, dit getalletje stelt als het ware de plaats op de regenboog voor. De tint geeft dus de kleur aan.
- Saturation (Sat) staat voor intensiteit. Wanneer dit getal groot is, is de kleur fel, een klein getal betekent weinig kleur. Je ziet de intensiteit van boven naar beneden teruglopen in het regenboogvlak.
- Luminance (Lum) geeft de helderheid aan, dat wil zeggen: het geeft aan hoe licht een kleur is. Dit kun je aangeven op de balk rechts.
RGB en HSL zijn verschillende manieren om dezelfde kleuren te beschrijven. Wanneer je iets verandert in de RGB-waarden, zullen de HSL-waarden mee veranderen en omgekeerd.
Vul nu bij rood 128, groen 128, blauw 128 in. Je krijgt grijs !
Maak nu de volgende tekening van 5 bij 3 (Klik eerst op Kenmerken en vul bij breedte 5 in en bij hoogte 3):
Klik op Bestand en dan op Opslaan als.
Vul in als bestandsnaam : Mozaiek
Kies bij Opslaan als Type : 24 bits
Klik dan op OK
Start dan het programma ASC, daarmee kun je bekijken hoe een bestand wordt opgeslagen.
Je kunt dat programma hier downloaden.
Als je het programma ASC geopend heb klik je op Bestand Openen, en open dan het bestand mozaiek.bmp dat je net met Paint hebt gemaakt.
Dan zie je hoe de computer het heeft opgeslagen, zie de figuur hieronder.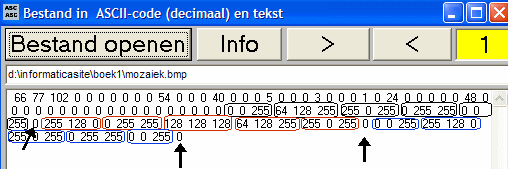
De eerste 54 getallen, die je ziet, bevatten algemene informatie over de figuur (bijvoorbeeld de lengte en de breedte, dus de getallen 5 en 3)
Dan zie je de getallen 0, 0 en 255, dat zijn de RGB-kleuren van de eerste pixel van de laatste rij. Er wordt dus begonnen met de pixels van de laatste rij. En de drie RGB-getallen worden in de omgekeerde volgorde opgeslagen, Blauw-Groen-Rood
Daarnaast zie je de RGB-waarden van de volgende vier pixels.
Daarna zie je een 0 (zie pijl), het einde van een rij pixels wordt blijkbaar aangegeven met een nul
Daarna komen de RGB-waarden van de vijf pixels van de vorige rij. En het einde van die rij wordt weer aangegeven met een nul.
Tenslotte zie je de RGB-waarden van de vijf pixels van de eerste rij. Ook het einde van die rij wordt weer aangegeven met een nul.
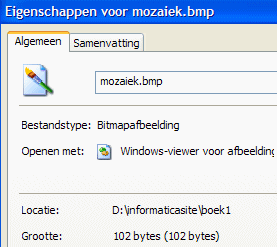
Als je daarna de Verkenner start kun je zien hoeveel bytes het bestand mozaiek.bmp in beslag neemt.
Klik met de rechter muis op de naam van het bestand, en klik in het snelmenu op Eigenschappen.
Dan zie je dat het bestand 102 bytes in beslag neemt.
Dat aantal kun je zelf berekenen:
15 x 3 =45 (15 pixels, die elk 3 bytes in beslag nemen)
54 (voor de algemene informatie van de figuur)
3 (elke rij wordt afgesloten met een 0), dus totaal 45 + 54 + 3 = 102

1.11 Compressie

Bestanden nemen vaak veel meer schijfruimte in beslag dan strikt noodzakelijk is.
Met de juiste software kan je zulke bestanden verkleinen (ook wel comprimeren genoemd), zodat ze veel minder plaats in beslag nemen. Dit wordt compressiesoftware genoemd.
In sommige gevallen worden de bestanden wel 90 % kleiner gemaakt.

De bekendste compressie-programma's zijn WinZIP (www.winzip.com), WinRAR (www.rarlab.com), IZArc (www.izarc.org), Winace (www.winace.com) en 7-Zip (www.7zip.com).

en Gegevenscompressie heeft niet alleen als voordeel dat er minder opslagruimte nodig is voor het bewaren van bestanden, het is ook mogelijk verschillende bestanden samen te voegen tot één gecomprimeerd bestand, waardoor het sneller en gemakkelijker via het internet te versturen is.
Bovendien scheelt dat veel extra ruimte, omdat als je veel kleine bestandjes hebt er heel veel ongebruikte schijfruimte (ook wel slack space genoemd) ontstaat. Want voor elk bestand wordt een geheel aantal clusters gebruikt (wat daarmee bedoeld wordt merk je wel als we met hoofdstuk 4 bezig zijn).

Een nadeel is dat, als je een gecomprimeerd bestand wilt openen, je het eerst uit moet pakken.
En dat betekent dat, als je zo'n gecomprimeerd bestand ontvangt, je wel de goede compressiesoftware moet hebben om het uit te kunnen pakken.

Hoe werkt compressiesoftware.
We leggen dit uit m.b.v. een voorbeeld, stel je voor dat een bestand de volgende zin bevat: ik zeg wat ik denk, en ik doe wat ik zeg.
Dit zinnetje neemt 41 bytes in beslag.
Verschillende woorden komen meer dan één keer voor in deze zin.
Er komt ook een woordcombinatie (twee woorden achter elkaar) in voor, namelijk "ik zeg".
De compressiesoftware gaat daarom de woorden wat, ik, denk, en, doe, en de woordcombinatie "ik zeg" opnemen in het "woordenboek".
Het woordenboek ziet er dan als volgt uit:

ik zeg
wat
ik
denk
en
doe

Het gecomprimeerde zinnetje wordt nu : 1 2 3 4, 5 3 6 2 1.
Het woordenboek neemt 7 + 4 + 3 + 5 + 3 + 4 = 26 bytes in beslag, en dan komen er nog 10 bytes bij, dus in totaal 36 bytes.
Zonder compressie was het 41 bytes. Dat scheelt in dit geval vrij weinig geheugenruimte, maar als je een groot bestand heb scheelt het soms wel 90%
De mate waarin een bestand wordt gecomprimeerd, wordt de compressieverhouding genoemd. Als de compressieverhouding 90 % is dan betekent het dat de grootte van het gecomprimeerde bestand maar 10 % is van het oorspronkelijke.

Een compressieprogramma zoekt dus voor elk bestand veel voorkomende patronen, en bouwt voor elk bestand een patronenlijst op. De manier waarop een programma dat doet, is erg ingewikkeld (en hoe het precies gaat is geheim), en is voor elk compressie-programma weer anders. Dat verklaart ook waarom eenzelfde bestand dat je met verschillende compressieprogramma's comprimeert, verschillende opslagruimtes oplevert.
De methode waarmee het gebeurt wordt het LZ Adaptive Dictionary-based algoritme genoemd.
LZ verwijst naar Lempel en Ziv, de uitvinders van de methode.
En Adaptive Dictionary-based verwijst naar de manier waarop de stukjes gegevens worden geordend.

Deze vorm van gegevenscompressie wordt lossless gegevenscompressie genoemd, een bestand wordt gecomprimeerd maar kan later weer tot op de bit nauwkeurig in zijn oorspronkelijke vorm worden uitgepakt.
Er bestaan compressiemethodes, zoals MP3, en JPG, waarbij wel informatie verloren gaat, dat wordt dan lossy gegevenscompressie genoemd.

1.12 Het jpg- ,gif- en png-formaat

In GIF-formaat en JPG-formaat nemen tekeningen en foto's veel minder ruimte in beslag dan in het BMP-formaat Er wordt van "compressie-technieken" gebruik gemaakt.

Er zijn vier heel bekende bestandsformaten voor plaatjes: bmp, jpg, gif en png.
Er wordt daarbij gebruik gemaakt van verschillende compressie-technieken, behalve bij het bmp-formaat.

bmp (bitmap) neemt veel te veel ruimte in beslag.
jpg (joint photographic experts group): heel geschikt voor foto's, meestal heb je dan veel kleurschakeringen relatief weinig scherpe kleurovergangen.
gif (graphics interchange format): heel geschikt voor zelfgemaakte tekeningen, als er grote vlakken met dezelfde kleur zijn. Het aantal kleuren is dan beperkt.
png (portable network graphics) is een formaat dat steeds meer gebruikt wordt. Het kan dienen als vervanger van het jpg- en het gif-formaat.
Commerciële gebruikers moeten officiëel betalen als ze op het internet gebruik maken van het gif- en/of jpg-formaat (of ze dat werkelijk doen is maar zeer de vraag trouwens), dat hoeft niet voor het png-formaat.

1.13 Het GIF-formaat (Graphics Interchange Format)

In een enkele afbeelding zullen lang niet alle mogelijke kleuren voorkomen.
Het kan ook zijn dat een deel van de afbeelding helemaal dezelfde kleur heeft, bijvoorbeeld een vlakje in één kleur.
Je kunt een programma een lijst laten maken van alle kleuren die voorkomen.
Kleuren die bijna hetzelfde zijn, kun je vervangen door één kleur.
Je krijgt zo een beetje kwaliteitsverlies, maar dit hoeft niet zo groot te zijn. Bij het gif-formaat wordt het aantal kleuren op die manier teruggebracht tot 256.

Van deze kleuren wordt een lijstje gemaakt: kleur 0 is één of andere RGB-waarde, kleur 1 is ...., tot en met kleur 255.
Het nummer van de kleur past in één byte. Bij de algemene informatie over de afbeelding wordt een lijstje met de 256 gebruikte kleuren geplaatst en voor ieder beeldpunt is dan nog maar één byte nodig om het vast te leggen: het nummer van de kleur.
Zo'n lijst van gebruikte kleuren heet een palet of kleurentabel of CLUT, colour lookup table. Hieronder zie je een voorbeeld van een palet.

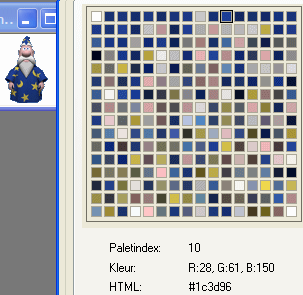
Verder wordt er gebruik gemaakt van de zogenaamde LZH-compressie (die ook bij bijv. WinZip wordt gebruikt) om ervoor te zorgen dat het bestand minder ruimte in beslag neemt.
Het GIF-formaat heeft nog twee bijzonderheden:

Je kunt een animated-gif maken: een bewegend plaatje
Je kunt bepaalde kleuren transparant maken, in dat gedeelte zie je dan de kleur van de achtergrond.

1.14 JPEG of JPG (Joint Photographic Experts Group)

Het JPEG algoritme verdeelt de foto in blokjes van pixels, die bij elkaar liggen en neemt het gemiddelde van de kleuren van de pixels uit dat blokje. Voor alle pixels uit dat blokje hoeft dus maar één kleur te worden vastgelegd.
Hoe groter de blokjes zijn, waarvan de kleur van de pixels gemiddeld wordt, hoe groter de compressieverhouding zal zijn. Maar als die verhouding te groot is neemt de beeldkwalitiet ook af.
Als je bijvoorbeeld het programma IrfanView gebruikt om een bestand als jpg-file op te slaan, dan kun je zelf aangeven in welke mate het gecomprimeerd moet worden.
Als je in het menu kiest voor File → Save as, je kiest voor opslaan als een JPG-file, en je klikt op Options (of bij een nieuwere versie zet je een vinkje voor Show options dialog), dan krijg je onderstaand venster in beeld.
Dan kun je m.b.v. een schuifbalkje de kwaliteit bij het opslaan aangeven. Als je die op 80 % zet zal de kwaliteit heel goed zijn.
Als je die op bijv. 50 % zet zal de kwaliteit wel iets minder zijn, maar is nog best aanvaardbaar.

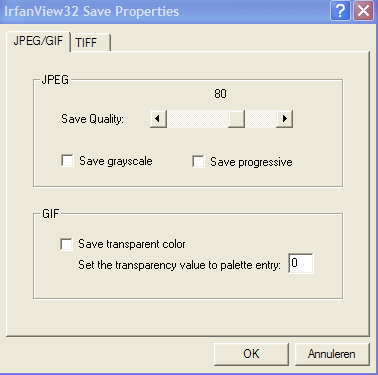
Nadat dit gebeurd is wordt het bestand ook nog gecomprimeerd met het LZH-algoritme (op ongeveer dezelfde manier waarop bijvoorbeeld WinZip comprimeert).

Het is niet verstandig een jpg-bestand te openen, bewerken en daarna weer bewaren als jpg-bestand. Want elke keer wanneer je een bestand bewaart als jpg wordt er informatie weggegooid.
Soms kan het niet anders, maar wel als je een bmp-bestand hebt met dezelfde foto. Als je een fout maakt tijdens het bewerken kun je beter weer met het orginele bmp-bestand beginnen. Omdat comprimeren tot een jpg-bestand lossy gegevenscompressie is, er gaat informatie verloren.

1.15 PNG (Portable Network Graphics)

PNG is door een aantal mensen bedacht toen het computerbedrijf Unisys bekend maakte dat ze voortaan geld zouden gaan vragen voor commercieel gebruik van de zogenaamde LZH-compressie (waar zij patent op hebben). Die LZH-compressie wordt o.a. gebruikt bij het gif- en het jpg-formaat.
PNG is een vrij te gebruiken bestandsformaat, het dient vooral als vervanger van het GIF-formaat. Het biedt een betere compressie dan GIF, dat scheelt vaak wel 30 %.
Met het formaat PNG kun je ook 24-bits-plaatjes opslaan, het kan dus ook als vervanger van het JPG-formaat dienen.
Een nadeel t.o.v. het GIF-formaat is dat je niet zoiets als animated-gifs met het PNG-formaat kunt maken.

1.16 Vector-geörienteerd

Tekeningen worden meestal opgeslagen als bitmap: de kleur van elk pixel wordt opgeslagen.
Een tekening kan ook op een andere manier worden opgeslagen: vector-geörienteerd.
Als je bijvoorbeeld een cirkel tekent dan bewaart het programma in dit geval niet het bitpatroon, maar een reeks getallen die de tekening vastleggen : een getal voor het type tekening (een cirkel in dit geval), de straal, de lijndikte, de kleur van de lijn, de kleur van de vulling, en de coördinaten van het middelpunt.
Powerpoint werkt bijv. vector-geörienteerd.

1.17 Geluid

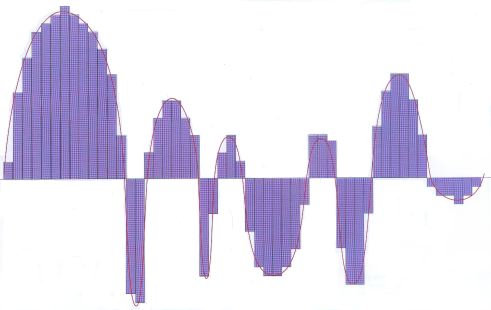
Geluid bestaat uit golven.
Je ziet hieronder de grafiek van een geluidsgolf; horizontaal is de tijd uitgezet.
De geluidsgolf kun je digitaliseren door met regelmatige tussenpozen de hoogte van de golf te meten.
Dit is in de afbeelding weergegeven door de paarse balken.
De hoogte van de balk is een getal. Op deze manier kun je geluid voorstellen door een reeks van getallen.
Dit noem je sampling.
Deze techniek voor het digitaliseren van geluid wordt ook toegepast in muziek-CD's.

Een geluids-bestand dat niet gecomprimeerd is heeft de extensie wav (van wave = golf) , maar dat neemt veel geheugenruimte in beslag: ongeveer 10 Mb per minuut bij CD kwaliteit.
Er wordt dan gesampled op 44.1 kHz, met 16 bits per sample ( dat is de audio-bandbreedte voor Compact Discs)
Dat betekent dat er 44100 keer per sec. de hoogte van de geluidsgolf wordt gemeten. En elke hoogte wordt opgeslagen in 2 bytes (daarom wordt het 16 bits genoemd).
Dat is dus 44100 x 2 x 60 bytes per minuut.
Meestal heb je stereo-geluid, dan komt het geluid via twee kanalen binnen en dan moet je het nog keer 2 doen. Dan kom je op 10.584.000 bytes per minuut, en dat is dus iets meer dan 10 Mb

Bij cd-kwaliteit wordt er gesampled op 44.1 kHz. Daardoor is de hoogste toon die gereproduceerd kan worden een toon met een frequentie van 22.05 kHz (de helft van 44.1). En die toon is de hoogste toon die het menselijk oor kan waarnemen.

Het zachtste geluid dat ons oor kan waarnemen is ruim 90 dB zachter dan het hardste geluid dat wij nog aankunnen (geluidssterkte wordt gemeten in dB = decibel).
Elke afname van het volume met 20 dB wordt door ons waargenomen als een 10 keer zo zacht geluid.
Een verschil van 90 dB komt dus ongeveer overeen met 4.5 keer de afname van een factor 10, dus in totaal met een factor 10^4.5 = 31622
Dat is de reden dat het geluid met 16 bits per sample wordt vastgelegd. Want met 16 bits (dus 2 bytes) kun je 256 x 256 = 65536 verschillende getallen vastleggen. Dat komt overeen met 32768 stappen boven en onder de horizontale as, dus ruim 90 dB.

Een ander formaat is het midi-formaat (.mid), dat is de afkorting van Music Instrumental Digital Interface.
Dat neemt minder ruimte in beslag dan een wav-bestand, maar dit formaat kan alleen voor muziek gebruikt worden.
Bij een mid-bestand worden namelijk eigenlijk de muzieknoten vastgelegd.
Een wav-bestand kan voor alle geluiden gebruikt worden, net zo als een au-bestand.
Het bekendste formaat waarin muziek vaak gecomprimeerd wordt opgeslagen is mp3
MP3 staat officieel voor Mpeg Layer 3.

Door gebruik te maken van de zogenaamde MPEG-compressie (MPEG is de afkorting van Moving Pictures Experts Group) kan een 12 voudige reductie worden bereikt bij handhaving van CD-geluidskwaliteit.
(Er is inmiddels al weer een nieuwe compressietechniek: MP3PRO Dit is een verbeterde versie van MP3. Het halveert de grootte van een bestand nog eens ten opzichte van MP3)
Alles wat niet voor het oor hoorbaar is wordt uit het oorspronkelijke signaal weggelaten. En er wordt een coderings-algoritme gebruikt.
Met behulp van een encoder programma is een wav-file in een mp3-file om te zetten. Zo'n programma is bv "MPEG layer-3 producer". Het decoder programma reconstrueert het oorspronkelijke audio signaal uit de mp3-file.
Een bekende MP3 decoder is Winamp, dat in staat is om tegelijkertijd het geluid te berekenen en af te spelen.

Ook tussen MP3's onderling bestaat weer kwaliteitsverschil. Een MP3 heeft altijd een bitrate, dat is een getal dat aangeeft hoeveel kilobits per seconde (Kbps) muziek gebruikt worden. Die bitrate kan variëren maar is meestal tussen de 128 en 192 Kbps.

1.18 Video

Bij video zijn er 25 beelden per seconde.
Hierboven heb je gezien dat een foto heel veel geheugenruimte in beslag neemt.
Voor digitale video geldt dat nog veel sterker, je hebt dan 25 beelden per seconde!

Videobestanden worden standaard opgeslagen als avi-bestand. (dat is de samentrekking van audio-video)
Dat kost ontzettend veel geheugenruimte.

Digitale video is daarom vooral een kwestie van compressie. Je moet bezuinigen op de hoeveelheid benodigd geheugen om digitale video mogelijk te maken.
De belangrijkste truc voor het bezuinigen werkt als volgt:
Wanneer je een video beeldje voor beeldje bekijkt, zul je zien dat er tussen twee opeenvolgende beeldjes meestal niet zo veel verschil is. In plaats van losse beeldjes achter elkaar vast te leggen, kun je een volgend beeldje beschrijven door als het ware te zeggen: "dit beeldje is hetzelfde als het vorige, maar met deze verschillen: ..."
Op deze manier kan er heel veel bespaard worden op de geheugenruimte die nodig is voor digitale video.
Dat gebeurt, net zoals bij muziek, meestal in het mpeg-formaat.

In MPEG1-formaat wordt het wel videoCD (VCD) genoemd.
Dat kost 10 Mb geheugenruimte per minuut film. Op een CDrom van 700 Mb past dan circa 70 minuten film, en op een DVD past dan ongeveer 8 uren film
In MPEG2-formaat wordt het wel supervideoCD (VCD) genoemd.
De beelden hebben dan een hogere resolutie. Dat kost ongeveer twee keer zoveel geheugenruimte als MPEG1
En dan heb je nog het MPEG4-formaat, ook wel divX genoemd.
De resolutie is dan nog hoger, en het kost meestal toch iets minder geheugenruimte dan MPEG1

Je hebt wel een codec nodig om zo'n film af te kunnen spelen.
Het woord "codec" is de afkorting van "compressor/decompressor". Die zorgt er voor dat Windows Media Player het videobestand al decoderend af kan spelen.